题目内容
已知函数f(x)=2cos2x+
sin2x.
(1)求f(x)的最小正周期和单调递增区间;
(2)若关于x的方程f(x)-m=2在x∈[-
,
]上有解,求实数m的取值范围.
| 3 |
(1)求f(x)的最小正周期和单调递增区间;
(2)若关于x的方程f(x)-m=2在x∈[-
| π |
| 4 |
| π |
| 4 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)化简可得f(x)=2sin(2x+
)+1,易得周期,解2kπ-
≤2x+
≤2kπ+
可得单调递增区间;
(2)由x∈[-
,
]可得sin(2x+
)的范围,进而可定的f(x)的值域,即m+2的范围,可得答案.
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
(2)由x∈[-
| π |
| 4 |
| π |
| 4 |
| π |
| 6 |
解答:
解:(1)化简可得f(x)=2cos2x+
sin 2x
=1+cos2 x+
sin 2x=1+2(
cos 2x+
sin 2x)
=2sin(2x+
)+1,
∴f(x)的最小正周期T=π,
令2kπ-
≤2x+
≤2kπ+
,k∈Z,
解得kπ-
≤x≤kπ+
,
f(x)的单调递增区间为[kπ-
,kπ+
,(k∈Z).
(2)∵x∈[-
,
],∴2x+
∈[-
,
],
∴sin(2x+
)∈[-
,1],
∴f(x)的值域为[1-
,3]
∵f(x)=m+2,∴m+2∈[1-
,3],
即m∈[-1-
,1].
| 3 |
=1+cos2 x+
| 3 |
| 1 |
| 2 |
| 3 |
=2sin(2x+
| π |
| 6 |
∴f(x)的最小正周期T=π,
令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得kπ-
| π |
| 3 |
| π |
| 6 |
f(x)的单调递增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
(2)∵x∈[-
| π |
| 4 |
| π |
| 4 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
∴sin(2x+
| π |
| 6 |
| ||
| 2 |
∴f(x)的值域为[1-
| 3 |
∵f(x)=m+2,∴m+2∈[1-
| 3 |
即m∈[-1-
| 3 |
点评:本题考查三角函数的性质,涉及和差角公式和三角函数的值域,属中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
函数f(x)=2x+4x-3的零点所在区间是( )
A、(
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(
|
 已知直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=
已知直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=

 如图,单位正方形OABC在二阶矩阵T的作用下,变成菱形OA1B1C1.
如图,单位正方形OABC在二阶矩阵T的作用下,变成菱形OA1B1C1.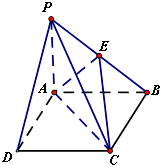 在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,
在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,