题目内容
某校新生入学时该校选取甲、乙两个高一新班(均为60人,入学数学平均分和优秀率都相同,勤奋程度和自觉性都一样)分别采用A,B两种方法教学,为了解A,B两种教学方法的效果,现随机抽取甲、乙两班各20名学生的市统考数学成绩(单位:分)如下:
甲班:58,57,59,92,71,82,65,82,74,67,74,67,68,85,83,78,81,69,73;
乙班:64,73,80,81,90,82,84,91,69,78,83,89,97,94,68,82,69,76,81,98.
(1)分别完成甲、乙两班各20名学生的市统考数学成绩的频率分布表,并作出频率分布直方图,根据频率分布直方图判断哪个班的优秀率高?(成绩大于等于80分为优秀)
甲班
乙班
(2)现从甲、乙两班各20名市统考数学成绩不低于85分的学生中各抽出2人,若成绩不低于90分的学生奖励100元,否则奖励50元,求奖金总数不少于310元的概率.
甲班:58,57,59,92,71,82,65,82,74,67,74,67,68,85,83,78,81,69,73;
乙班:64,73,80,81,90,82,84,91,69,78,83,89,97,94,68,82,69,76,81,98.
(1)分别完成甲、乙两班各20名学生的市统考数学成绩的频率分布表,并作出频率分布直方图,根据频率分布直方图判断哪个班的优秀率高?(成绩大于等于80分为优秀)
甲班
| 分组 | 频数 | 频率 |
| [90,100] | ||
| [80,90) | ||
| [70,80) | ||
| [60,70) | ||
| [50,60) |
| 分组 | 频数 | 频率 |
| [90,100] | ||
| [80,90) | ||
| [70,80) | ||
| [60,70) | ||
| [50,60) |

(2)现从甲、乙两班各20名市统考数学成绩不低于85分的学生中各抽出2人,若成绩不低于90分的学生奖励100元,否则奖励50元,求奖金总数不少于310元的概率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(1)由已知中数据计算出各组的频率,除以样本容量后得到各级的频率,除以组距后可得各组的高,可画出甲、乙两班各20名学生的市统考数学成绩的频率分布表,并作出频率分布直方图,进而计算出两个班的优秀率,比较后可得答案.
(2)奖金总数不少于310元的情况只可能是350元,即甲班两人均被抽中,乙班被抽中的2人的成绩不低于90分,计算出从乙班的6个人中抽取两人的方法总数,和从不低于90分的5人中抽取两人方法个数,代入古典概型概率计算公式,可得答案.
(2)奖金总数不少于310元的情况只可能是350元,即甲班两人均被抽中,乙班被抽中的2人的成绩不低于90分,计算出从乙班的6个人中抽取两人的方法总数,和从不低于90分的5人中抽取两人方法个数,代入古典概型概率计算公式,可得答案.
解答:
解:(1)甲、乙两班各20名学生的市统考数学成绩的频率分布表,如下所示:
甲班
乙班
甲、乙两班各20名学生的市统考数学成绩的频率分布直方图如下所示:
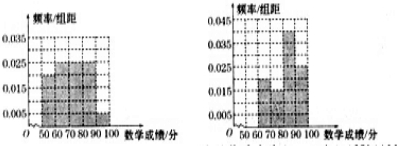
甲班的优秀率为(0.025+0.005)×10=0.3,
乙班的优秀率为(0.040+0.025)×10=0.65,
所以乙班的优秀率高.
(2)甲班统考数学成绩不低于85分的有92,85,
乙班统考数学成绩不低于85分的有90,91,89,97,94,98,
奖金总数不少于310元的情况只可能是350元,
即甲班两人均被抽中,乙班被抽中的2人的成绩不低于90分,
从乙班的6个人中抽取两人共有:
=15种不同的方法,
其中从不低于90分的5人中抽取两人共有:
=10种不同的方法,
故奖金总数不少于310元的概率P=
=
甲班
| 分组 | 频数 | 频率 | ||
| [90,100] | 1 |
| ||
| [80,90) | 5 |
| ||
| [70,80) | 5 |
| ||
| [60,70) | 5 |
| ||
| [50,60) | 4 |
|
| 分组 | 频数 | 频率 | ||
| [90,100] | 5 |
| ||
| [80,90) | 8 |
| ||
| [70,80) | 3 |
| ||
| [60,70) | 4 |
| ||
| [50,60) | 0 | 0 |

甲班的优秀率为(0.025+0.005)×10=0.3,
乙班的优秀率为(0.040+0.025)×10=0.65,
所以乙班的优秀率高.
(2)甲班统考数学成绩不低于85分的有92,85,
乙班统考数学成绩不低于85分的有90,91,89,97,94,98,
奖金总数不少于310元的情况只可能是350元,
即甲班两人均被抽中,乙班被抽中的2人的成绩不低于90分,
从乙班的6个人中抽取两人共有:
| C | 2 6 |
其中从不低于90分的5人中抽取两人共有:
| C | 2 5 |
故奖金总数不少于310元的概率P=
| 10 |
| 15 |
| 2 |
| 3 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
已知m,n是不同的两条直线,α,β是不同的两个平面,则下列命题中不正确的是( )
| A、若m∥n,m⊥α,则n⊥α |
| B、若m∥α,α∩β=n,则m∥n |
| C、若m⊥α,m?β,则α⊥β |
| D、若m⊥α,m⊥β,则α∥β |

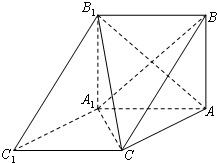 如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2
如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2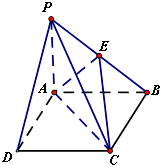 在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,
在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点, 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1,点E在SD上,且AE⊥SD.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1,点E在SD上,且AE⊥SD.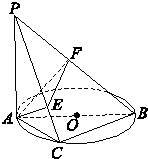 如图所示,已知PA⊥⊙O所在平面,AB是⊙O的直径,点C是⊙O上任意一点,过A作AE⊥PC于点E,AF⊥PB于点F,求证:
如图所示,已知PA⊥⊙O所在平面,AB是⊙O的直径,点C是⊙O上任意一点,过A作AE⊥PC于点E,AF⊥PB于点F,求证: 已知一几何体的三视图如图所示,点F,G分别为AC,DE的中点.
已知一几何体的三视图如图所示,点F,G分别为AC,DE的中点.