题目内容
对于函数f(x),若存在x0∈R,使得f(x0)=x0成立,则称x0为f(x)的不动点.已知二次函数f(x)=ax2+bx+c(a>0),满足
,且f(x)有两个不动点x1,x2,记函数f(x)的对称轴为x=x0,求证:如果x1<2<x2<4,那么x0>-1.
|
考点:二次函数的性质
专题:函数的性质及应用
分析:由已知求出c=1后,进而根据有x1<2<x2<4转化为g(x)=f(x)-x=0有两根:一根在2与4之间,另一根在2的左边,利用一元二次方程根的分布可证.
解答:
证明:二次函数f(x)=ax2+bx+c(a>0),满足
,
∴
,即f(0)=1,
∴f(x)=ax2+bx+1,
设g(x)=f(x)-x=ax2+(b-1)x+1,
∵a>0,
∴由条件x1<2<x2<4,
得g(2)<0,g(4)>0.
即
,

由可行域可得
<2,
∴x0=-
>-1.
|
∴
|
∴f(x)=ax2+bx+1,
设g(x)=f(x)-x=ax2+(b-1)x+1,
∵a>0,
∴由条件x1<2<x2<4,
得g(2)<0,g(4)>0.
即
|

由可行域可得
| b |
| a |
∴x0=-
| b |
| 2a |
点评:考查学生方程与函数综合运用的能力,分类讨论的数学思想,以及灵活运用不等式解决数学问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
二项式(2x+
)6展开式中的常数项是( )
| 1 | ||
|
| A、15 | B、60 |
| C、120 | D、240 |
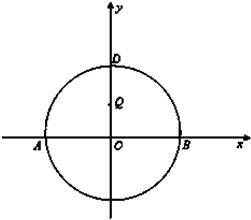 如图,AB为圆O直径,已知A(-2,0)、B(2,0),D为圆O上的一点,且
如图,AB为圆O直径,已知A(-2,0)、B(2,0),D为圆O上的一点,且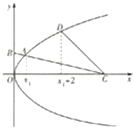 抛物线M:y2=2px(p>0)的准线过椭圆N:
抛物线M:y2=2px(p>0)的准线过椭圆N: