题目内容
根据表格中的数据，可以断定方程ex-（2x+4）=0（e≈2.72）的一个根所在的区间是（ ）
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.70 | 7.29 | 19.68 |
| 2x+4 | 2 | 4 | 6 | 8 | 10 |
| A、（-1，0） |
| B、（0，1） |
| C、（1，2） |
| D、（2，3） |
考点：根的存在性及根的个数判断
专题：计算题,函数的性质及应用
分析：令g（x）=ex-（2x+4），则g（-1）＜0，g（0）＜0，g（1）＜0，g（2）＜0，g（3）＞0，由零点存在定理，即可判断．
解答：
解：令g（x）=ex-（2x+4），
则g（-1）＜0，g（0）＜0，g（1）＜0，g（2）＜0，g（3）＞0，
即有g（2）g（3）＜0，由零点存在定理，
可得在区间（2，3）上存在零点，
故选：D．
则g（-1）＜0，g（0）＜0，g（1）＜0，g（2）＜0，g（3）＞0，
即有g（2）g（3）＜0，由零点存在定理，
可得在区间（2，3）上存在零点，
故选：D．
点评：本题考查函数的零点的判断，考查函数的零点存在定理的运用，属于基础题．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
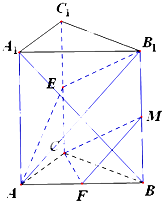如图直三棱柱ABC-A1B1C1，CA=CB，E、F、M分别是棱CC1、AB、BB1中点．
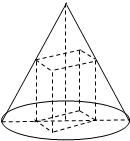底面半径为2，高为4