题目内容
已知变量x,y满足约束条件为
,若目标函数z=ax+y(a>0)仅在点(4,0)处取得最大值,则a的取值范围为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式对应的平面区域,利用线性规划的知识,确定目标取最优解的条件,即可求出a的取值范围.
解答:
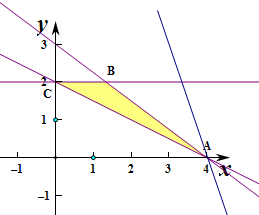 解:作出不等式组对应的平面区域如图:(阴影部分).
解:作出不等式组对应的平面区域如图:(阴影部分).
由z=ax+y(a>0)得y=-ax+z,
∵a>0,∴目标函数的斜率k=-a<0.
平移直线y=-ax+z,
要使目标函数z=ax+y(a>0)仅在点(4,0)处取得最大值,
则目标函数的斜率k=-a<-
,
即a>-
,
故答案为:(-
,+∞)
 解:作出不等式组对应的平面区域如图:(阴影部分).
解:作出不等式组对应的平面区域如图:(阴影部分).由z=ax+y(a>0)得y=-ax+z,
∵a>0,∴目标函数的斜率k=-a<0.
平移直线y=-ax+z,
要使目标函数z=ax+y(a>0)仅在点(4,0)处取得最大值,
则目标函数的斜率k=-a<-
| 3 |
| 4 |
即a>-
| 3 |
| 4 |
故答案为:(-
| 3 |
| 4 |
点评:本题主要考查线性规划的应用,利用数形结合是解决线性规划题目的常用方法.根据条件目标函数z=ax+y仅在点A(4,0)处取得最大值,确定直线的位置是解决本题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
根据表格中的数据,可以断定方程ex-(2x+4)=0(e≈2.72)的一个根所在的区间是( )
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.70 | 7.29 | 19.68 |
| 2x+4 | 2 | 4 | 6 | 8 | 10 |
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
用秦九韶算法求多项式f(x)=4x5-3x4+6x-9,当x=-3时的值时,需要乘法运算和加法运算的次数分别为( )
| A、4,2 | B、5,3 |
| C、5,5 | D、5,4 |
 已知奇函数f(x)的定义域为{x|x≠0,x∈R},在y轴右侧的图象如图,且f(3)=0,则不等式f(x)<0的解集为
已知奇函数f(x)的定义域为{x|x≠0,x∈R},在y轴右侧的图象如图,且f(3)=0,则不等式f(x)<0的解集为