题目内容
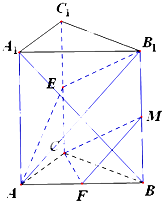 如图直三棱柱ABC-A1B1C1,CA=CB,E、F、M分别是棱CC1、AB、BB1中点.
如图直三棱柱ABC-A1B1C1,CA=CB,E、F、M分别是棱CC1、AB、BB1中点.(1)求证:平面AEB1∥平面CFM;
(2)求证:CF⊥BA1.
考点:直线与平面垂直的性质,平面与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)利用平面与平面平行的判定定理可得结论;
(2)证明CF⊥平面ABB1A1,即可证明CF⊥BA1.
(2)证明CF⊥平面ABB1A1,即可证明CF⊥BA1.
解答:
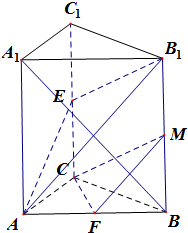 证明:(1)∵B1M∥CE,且B1M=CE,
证明:(1)∵B1M∥CE,且B1M=CE,
∴四边形CEB1M是平行四边形,
∴CE∥EB1
又∵FM∥AB1,
CF∩FM=M,EB1∩AB1=B1,
∴平面AEB1∥平面CFM;
(2)直三棱柱ABC-A1B1C1,BB1⊥平面ABC,
∴BB1⊥CF,
∵AC=BC,AF=FB,
∴CF⊥AB,BB1∩AB=B,
∴CF⊥平面ABB1A1,
∴CF⊥BA1.
 证明:(1)∵B1M∥CE,且B1M=CE,
证明:(1)∵B1M∥CE,且B1M=CE,∴四边形CEB1M是平行四边形,
∴CE∥EB1
又∵FM∥AB1,
CF∩FM=M,EB1∩AB1=B1,
∴平面AEB1∥平面CFM;
(2)直三棱柱ABC-A1B1C1,BB1⊥平面ABC,
∴BB1⊥CF,
∵AC=BC,AF=FB,
∴CF⊥AB,BB1∩AB=B,
∴CF⊥平面ABB1A1,
∴CF⊥BA1.
点评:本题考查平面与平面平行的判定定理,考查线面垂直的判定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
已知直线m,n,l,若m∥n,n∩l=P,则m与l的位置关系是( )
| A、异面直线 |
| B、相交直线 |
| C、平行直线 |
| D、相交直线或异面直线 |
根据表格中的数据,可以断定方程ex-(2x+4)=0(e≈2.72)的一个根所在的区间是( )
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.70 | 7.29 | 19.68 |
| 2x+4 | 2 | 4 | 6 | 8 | 10 |
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
用秦九韶算法求多项式f(x)=4x5-3x4+6x-9,当x=-3时的值时,需要乘法运算和加法运算的次数分别为( )
| A、4,2 | B、5,3 |
| C、5,5 | D、5,4 |
 已知奇函数f(x)的定义域为{x|x≠0,x∈R},在y轴右侧的图象如图,且f(3)=0,则不等式f(x)<0的解集为
已知奇函数f(x)的定义域为{x|x≠0,x∈R},在y轴右侧的图象如图,且f(3)=0,则不等式f(x)<0的解集为