Question

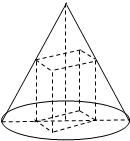底面半径为2，高为4

2

的圆锥有一个内接的正四棱柱（底面是正方形，侧棱与底面垂直的四棱柱）．
（1）设正四棱柱的底面边长为x，试将棱柱的高h表示成x的函数；
（2）当x取何值时，此正四棱柱的表面积最大，并求出最大值．

Answer 1

考点：函数的最值及其几何意义,函数解析式的求解及常用方法

专题：计算题,函数的性质及应用,空间位置关系与距离

分析：（1）由相似性可得

2 2 x

2

=

4 2 -h

4 2

，从而化出h=4

2

-2x，（其中0＜x＜2

2

）；
（2）设该正四棱柱的表面积为y，则y=2x²+4xh=2x²+4x（4

2

-2x）=-6x²+16

2

x，利用配方法求函数的最大值．

解答： 解：（1）根据相似性可得：

2 2 x

2

=

4 2 -h

4 2

，
解得：h=4

2

-2x，（其中0＜x＜2

2

）．
（2）解：设该正四棱柱的表面积为y．则有关系式：
y=2x²+4xh=2x²+4x（4

2

-2x）
=-6x²+16

2

x
=-6（x-

4

3

2

）²+

64

3

，
因为0＜x＜2

2

，
所以当x=

4

3

2

时，
y_max=

64

3

，
故当正四棱柱的底面边长为

4

3

2

时，此正四棱柱的表面积最大，为

64

3

．

点评：本题考查了空间几何体的结构特征及函数的最值问题，属于中档题．