题目内容
8.设函数f(x)的定义域为D,如果存在正实数k,使对任意x∈D,都有x+k∈D,且f(x+k)>f(x)恒成立,则称函数f(x)为D上的“k型增函数”.已知f(x)是定义在R上的奇函数,且当x>0时,f(x)=|x-a|-2a,若f(x)为R上的“2 015型增函数”,则实数a的取值范围是( )| A. | (-∞,$\frac{2015}{4}$) | B. | ($\frac{2015}{4}$,+∞) | C. | (-∞,$\frac{2015}{6}$) | D. | ($\frac{2015}{6}$,+∞) |
分析 利用奇函数的性质可得f(x)的解析式,再利用新定义对x分类讨论和绝对值的意义即可得出.
解答 解:∵f(x)是定义在R上的奇函数,
∴f(0)=0.
设x<0,则-x>0.
∴f(-x)=|-x-a|-2a=|x+a|-2a,
∴f(x)=-f(-x)=-|x+a|+2a.
∴f(x)=$\left\{\begin{array}{l}|x-a|-2a,x>0\\ 0,x=0\\-|x-a|+2a,x<0\end{array}\right.$.
分类讨论:
①当x>0时,由f(x+2015)>f(x),可得|x+2015-a|-2a>|x-a|-2a,化为|x-(a-2015)|>|x-a|,由绝对值的几何意义可得a+a-2015<0,解得a<$\frac{2015}{2}$.
②当x<0时,由f(2015+x)>f(x),
分为以下两类研究:当x+2015<0时,可得-|x+2015+a|+2a>-|x+a|+2a,化为|x+2015+a|<|x+a|,由绝对值的几何意义可得-a-a-2015>0,解得a<-$\frac{2015}{2}$.
当x+2015>0,|x+2015-a|-2a>-|x+a|+2a,化为|x+2015-a|+|x+a|≥|2015-2a|>4a,a≤0时成立;
当a>0时,a<$\frac{2015}{6}$,因此可得a<$\frac{2015}{6}$.
③当x=0时,由f(2015)>f(0)可得|2015-a|-2a>0,当a≤0时成立,当a>0时,a<$\frac{2015}{3}$.
综上可知:a的取值范围是a<$\frac{2015}{6}$.
故答案为(-∞,$\frac{2015}{6}$),
故选:C
点评 本题考查了奇函数的性质、新定义、分类讨论和绝对值的意义等基础知识与基本技能方法,属于难题

| A. | $\frac{{6\sqrt{13}}}{13}$ | B. | $\frac{{6\sqrt{7}}}{7}$ | C. | $\frac{{6\sqrt{11}}}{11}$ | D. | $\sqrt{3}$ |
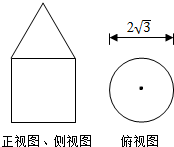 如图,一个简单组合体的正视图和侧视图都是由一个正方形与一个正三角形构成的相同的图形,俯视图是一个半径为$\sqrt{3}$的圆(包括圆心).则该组合体的表面积(各个面的面积的和)等于21π.
如图,一个简单组合体的正视图和侧视图都是由一个正方形与一个正三角形构成的相同的图形,俯视图是一个半径为$\sqrt{3}$的圆(包括圆心).则该组合体的表面积(各个面的面积的和)等于21π.