题目内容
已知数列{an}的前三项分别为a1=
,a2=
,a3=
,(其中λ为正常数).设f(x)=a12x+a22x2+a32x3+…an2xn.
(1)归纳出数列{an}的通项公式,并证明数列{an}不可能为等比数列;
(2)若λ=1,求f(2)的值;
(3)若λ=4,试证明:当n≥2时,an+1+an-1<2an.
| λ |
| λ+2 |
| λ+4 |
(1)归纳出数列{an}的通项公式,并证明数列{an}不可能为等比数列;
(2)若λ=1,求f(2)的值;
(3)若λ=4,试证明:当n≥2时,an+1+an-1<2an.
考点:归纳推理,等比关系的确定
专题:等差数列与等比数列,推理和证明
分析:(1)由已知中a1=
,a2=
,a3=
,可知数列被开方数是一个以λ为首项,以2为公差的等差数列,进而归纳出数列{an}的通项公式,进而根据等比数列的定义,可得数列{an}不可能为等比数列;
(2)若λ=1,可得数列{an}的通项公式,进而得到f(x)的表达式,利用错位相减法,可得f(2)的值;
(3)若λ=4,可得数列{an}的通项公式,进而利用分析法可证得当n≥2时,an+1+an-1<2an.
| λ |
| λ+2 |
| λ+4 |
(2)若λ=1,可得数列{an}的通项公式,进而得到f(x)的表达式,利用错位相减法,可得f(2)的值;
(3)若λ=4,可得数列{an}的通项公式,进而利用分析法可证得当n≥2时,an+1+an-1<2an.
解答:
解:(1)数列{an}的通项公式为an=
. …(2分)
下面证明数列{an}不可能为等比数列:
假设数列{an}为等比数列,则a22=a1a3,
即
2=
(λ>0),
即
=
(λ>0),
由λ2+4λ+4≠λ2+4λ,
故数列{an}不可能为等比数列;
(2)若λ=1,则an=
,
则an2=2n-1,
∴f(x)=x+3x2+5x3+…+(2n-1)xn.
∴f(2)=1×2+3×22+5×23+…+(2n-3)×2n-1+(2n-1)×2n.…①,
∴2f(2)=2×2+3×23+5×24+…+(2n-3)×2n+(2n-1)×2n+1.…②,
①-②得:
-f(2)=2+2(22+23+…+2n)-(2n-1)×2n+1=(1-n)2n+2+2n+1-6.
∴f(2)=(n-1)2n+2-2n+1+6.
(3)若λ=4,an=
当n≥2时,欲证 an+1+an-1<2an,
只需证
+
<2
只需证
2+2
•
+
2<4
2
只需证
<n+1
只需证
2<(n+1)2
只需证 0<1
显然 不等式0<1成立,
因此 当n≥2时,an+1+an-1<2an. …(14分)
| 2n+λ-2 |
下面证明数列{an}不可能为等比数列:
假设数列{an}为等比数列,则a22=a1a3,
即
| λ+2 |
| λ |
| λ+4 |
即
| λ2+4λ+4 |
| λ2+4λ |
由λ2+4λ+4≠λ2+4λ,
故数列{an}不可能为等比数列;
(2)若λ=1,则an=
| 2n-1 |
则an2=2n-1,
∴f(x)=x+3x2+5x3+…+(2n-1)xn.
∴f(2)=1×2+3×22+5×23+…+(2n-3)×2n-1+(2n-1)×2n.…①,
∴2f(2)=2×2+3×23+5×24+…+(2n-3)×2n+(2n-1)×2n+1.…②,
①-②得:
-f(2)=2+2(22+23+…+2n)-(2n-1)×2n+1=(1-n)2n+2+2n+1-6.
∴f(2)=(n-1)2n+2-2n+1+6.
(3)若λ=4,an=
| 2n+2 |
当n≥2时,欲证 an+1+an-1<2an,
只需证
| 2n+4 |
| 2n |
| 2n+2 |
只需证
| 2n+4 |
| 2n+4 |
| 2n |
| 2n |
| 2n+2 |
只需证
| n2+2n |
只需证
| n2+2n |
只需证 0<1
显然 不等式0<1成立,
因此 当n≥2时,an+1+an-1<2an. …(14分)
点评:本题考查的知识点是归纳推理,等比数列的证明,数列求和,不等式证明,是数列,不等式,函数,推理与证明的综合应用,综合性强,难度大.

练习册系列答案
相关题目
在△ABC中,“cosA=cosB”是“sinA=sinB”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
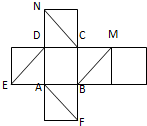 如图是正方体的平面展开图,在这个正方体中;
如图是正方体的平面展开图,在这个正方体中;(1)CN与AF平行;
(2)CN与BE是异面直线;
(3)CN与BM成60°;
(4)DE与BM垂直.
以上四个命题中,正确命题的序号是( )
| A、(1)(2)(3) |
| B、(2)(4) |
| C、(3)(4) |
| D、(3) |

 已知函数f(x)=|x2-2x|.
已知函数f(x)=|x2-2x|.