题目内容
已知a、b、c为正实数,且2a+b=1,则s=2
-5a2-b2-c2+2ac的最大值为( )
| ab |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:平均值不等式在函数极值中的应用
专题:不等式的解法及应用
分析:将原式看成是关于c的函数,对c进行配方,再利用基本不等式研究关于a、b的不等关系,得到原函数的最大值.
解答:
解:∵a、b、c为正实数,且2a+b=1,
∴2a+b≥2
,1≥2
,
即2
≤
(当且仅当2a=b时取等号).
又(2a+b)2≤2[(2a)2+b2],
∴4a2+b2≥
.
即-(4a2+b2)≤-
(当且仅当2a=b时取等号).
∴s=2
-5a2-b2-c2+2ac
=-c2+2ac-5a2+2
-b2
=-(c-a)2-(4a2+b2)+2
.
∵-(c-a)2≤0,
∴s≤0-
+
=
.(当且仅当2a=b时取等号).
∴s的最大值为
.
故选A.
∴2a+b≥2
| 2ab |
| 2ab |
即2
| ab |
| ||
| 2 |
又(2a+b)2≤2[(2a)2+b2],
∴4a2+b2≥
| 1 |
| 2 |
即-(4a2+b2)≤-
| 1 |
| 2 |
∴s=2
| ab |
=-c2+2ac-5a2+2
| ab |
=-(c-a)2-(4a2+b2)+2
| ab |
∵-(c-a)2≤0,
∴s≤0-
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴s的最大值为
| ||
| 2 |
故选A.
点评:本题考查了函数的最大值求法和基本不等式的应用,解题时要注意用基本不等式时的条件“一正二定三相等”,特别要注意同时取等号的条件.本题思维量不大,但有一定的运算量,属于中档题.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
某人计划年初向银行贷款m万元用于买房.他选择10年期贷款,偿还贷款的方式为:分10次等额归还,每年一次,并从借后次年年初开始归还,若10年期贷款的年利率为r,且每年利息均按复利计算(即本年的利息计入次年的本金生息),则每年应还款金额为( )元.
A、
| ||
B、
| ||
C、
| ||
D、
|
下表是甲、乙两个班级进行数学考试,按学生考试及格及不及格统计成绩后的2×2列联表:则X2的值为( )
| 不及格 | 及格 | 合计 | |
| 甲班 | 12 | 33 | 45 |
| 乙班 | 9 | 36 | 45 |
| 合计 | 21 | 69 | 90 |
| A、0.559 | B、0.456 |
| C、0.443 | D、0.4 |
一个正方体内接于一个球,过这个球的球心作一平面,则截面图形不可能是( )
A、 |
B、 |
C、 |
D、 |
将正方形ABCD沿对角线BD折成一个直二面角,点C到达点C1,则异面直线AB与C1D所成角是( )
| A、90° | B、60° |
| C、45° | D、30° |
当x∈[1,2]时,函数f(x)=ax2+4(a+1)x-3在x=2时取得最大值,则实数a的取值范围是( )
A、[-
| ||
| B、[0,+∞) | ||
| C、[1,+∞) | ||
D、[
|
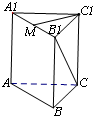 如图,在直三棱柱ABC-A1B1C1的底面ABC中,CA=CB=1,∠BCA=90°,AA1=2,点M是A1B1的中点,则异面直线C1M与B1C所成角的余弦值为( )
如图,在直三棱柱ABC-A1B1C1的底面ABC中,CA=CB=1,∠BCA=90°,AA1=2,点M是A1B1的中点,则异面直线C1M与B1C所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,已知a=
,b=
,B=45°,则角A为( )
| 3 |
| 2 |
| A、60° |
| B、150° |
| C、60°或 150° |
| D、60°或120° |