题目内容
定义在(-1,1)上的单调函数f(x)=
为奇函数,且f(
)=
.
(Ⅰ)求f(x)的解析式;
(Ⅱ)解不等式f(t-1)+f(t)<0.
| ax+b |
| x2+1 |
| 1 |
| 2 |
| 2 |
| 5 |
(Ⅰ)求f(x)的解析式;
(Ⅱ)解不等式f(t-1)+f(t)<0.
考点:函数奇偶性的性质,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:由于函数f(x)=
为奇函数,故f(0)=0,再结合f(
)=
解出a,b,从而求出函数的解析式;由函数的奇偶性,把不等式f(t-1)+f(t)<0转化为f(t-1)<f(-t),利用函数的单调性进行求解.
| ax+b |
| x2+1 |
| 1 |
| 2 |
| 2 |
| 5 |
解答:
解:(Ⅰ)有题意得:f(0)=0,得b=0,
又f(
)=
=
,解得a=1;
∴f(x)=
;
(Ⅱ)因为f(x)为单调函数,且f(
)=
>f(0),
所以f(x)在(-1,1)上是增函数,
由f(t-1)<-f(t),
即f(t-1)<f(-t),
所以
,
解得:0<t<
.
又f(
| 1 |
| 2 |
| ||
|
| 2 |
| 5 |
∴f(x)=
| x |
| x2+1 |
(Ⅱ)因为f(x)为单调函数,且f(
| 1 |
| 2 |
| 2 |
| 5 |
所以f(x)在(-1,1)上是增函数,
由f(t-1)<-f(t),
即f(t-1)<f(-t),
所以
|
解得:0<t<
| 1 |
| 2 |
点评:本题主要考察函数的单调性和奇偶性,注意奇函数中f(0)=0,属于基础题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
在直角坐标系xOy中,圆C的参数方程
(φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系,则圆C的极坐标方程是( )
|
| A、ρ=2cosθ |
| B、ρ=2sinθ |
| C、ρ=cosθ |
| D、ρ=sinθ |
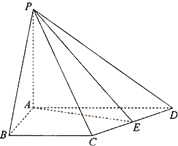 如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是D的中点.证明:CD⊥平面PAE.
如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是D的中点.证明:CD⊥平面PAE.