题目内容
已知圆C的方程x2+y2-2x+4y-m=0.
(1)若点A(m,-2)在圆C的内部,求m的取值范围;
(2)若当m=4时①设P(x,y)为圆C上的一个动点,求(x-4)2+(y-2)2的最值;②问是否存在斜率是1的直线l,使l被圆C截得的弦AB,以AB为直径的圆经过原点,若存在,写出直线l的方程;若不存在,说明理由.
(1)若点A(m,-2)在圆C的内部,求m的取值范围;
(2)若当m=4时①设P(x,y)为圆C上的一个动点,求(x-4)2+(y-2)2的最值;②问是否存在斜率是1的直线l,使l被圆C截得的弦AB,以AB为直径的圆经过原点,若存在,写出直线l的方程;若不存在,说明理由.
考点:直线与圆的位置关系,点与圆的位置关系
专题:直线与圆
分析:(1)根据圆C的标准方程可得m>-5.再根据点A(m,-2)在圆C的内部,可得 (m-1)2+(-2+2)2<5+m,由此求得m的范围.
(2)①(x-4)2+(y-2)2表示圆C上的点P(x,y)到点H(4,2)的距离的平方,求得|HC|=5,故(x-4)2+(y-2)2的最大值为HC加上半径后的平方,的最小值为HC减去半径后的平方.
②假设存在直线l满足题设条件,设l的方程为y=x+m,则AB中点N是两直线x-y+m=0与y+2=-(x-1)的交点,即N(-
,
),以AB为直径的圆经过原点,求得|AN|=
,|ON|=
,由|AN|=|ON|,解得m的值,可得结论.
(2)①(x-4)2+(y-2)2表示圆C上的点P(x,y)到点H(4,2)的距离的平方,求得|HC|=5,故(x-4)2+(y-2)2的最大值为HC加上半径后的平方,的最小值为HC减去半径后的平方.
②假设存在直线l满足题设条件,设l的方程为y=x+m,则AB中点N是两直线x-y+m=0与y+2=-(x-1)的交点,即N(-
| m+1 |
| 2 |
| m-1 |
| 2 |
9-
|
(-
|
解答:
解:(1)圆C的方程即(x-1)2+(y+2)2=5+m,∴m>-5.
再根据点A(m,-2)在圆C的内部,可得 (m-1)2+(-2+2)2<5+m,求得-1<m<4.
(2)①当m=4时,圆C的方程即(x-1)2+(y+2)2=5+4=9,而(x-4)2+(y-2)2表示圆C上的点P(x,y)到点H(4,2)的距离的平方,
由于|HC|=
=5,故(x-4)2+(y-2)2的最大值为 (5+3)2=64,(x-4)2+(y-2)2的最小值为 (5-3)2=4.
②假设存在直线l满足题设条件,设l的方程为y=x+m,圆C化为(x-1)2+(y+2)2=9,圆心C(1,-2),
则AB中点N是两直线x-y+m=0与y+2=-(x-1)的交点,即N(-
,
),以AB为直径的圆经过原点,
∴|AN|=|ON|,又CN⊥AB,|CN|=
,∴|AN|=
.
又|ON|=
,由|AN|=|ON|,解得m=-4或m=1.
∴存在直线l,其方程为y=x-4或y=x+1.
再根据点A(m,-2)在圆C的内部,可得 (m-1)2+(-2+2)2<5+m,求得-1<m<4.
(2)①当m=4时,圆C的方程即(x-1)2+(y+2)2=5+4=9,而(x-4)2+(y-2)2表示圆C上的点P(x,y)到点H(4,2)的距离的平方,
由于|HC|=
| (4-1)2+(2+2)2 |
②假设存在直线l满足题设条件,设l的方程为y=x+m,圆C化为(x-1)2+(y+2)2=9,圆心C(1,-2),
则AB中点N是两直线x-y+m=0与y+2=-(x-1)的交点,即N(-
| m+1 |
| 2 |
| m-1 |
| 2 |
∴|AN|=|ON|,又CN⊥AB,|CN|=
| |1+2+m| | ||
|
9-
|
又|ON|=
(-
|
∴存在直线l,其方程为y=x-4或y=x+1.
点评:本题主要考查点与圆的位置关系的判定,两点间的距离公式的应用,直线与圆相交的性质,属于基础题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
已知函数sgn(x)=
,则sgn(sgn(a2-a+1))的值是( )
|
| A、a2-a+1 |
| B、1 |
| C、0 |
| D、-1 |
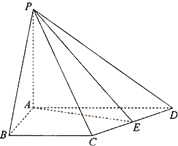 如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是D的中点.证明:CD⊥平面PAE.
如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是D的中点.证明:CD⊥平面PAE.