题目内容
已知函数f(x)=x4-4x3-4x2-1.
(1)设g(x)=bx2-1,若方程f(x)=g(x)的解集恰好有3个元素,求b的取值范围;
(2)在(1)的条件下,是否存在实数对(m,n),使f(x-m)+g(x-n)为偶函数?如存在,求出m、n;如不存在,说明理由.
(1)设g(x)=bx2-1,若方程f(x)=g(x)的解集恰好有3个元素,求b的取值范围;
(2)在(1)的条件下,是否存在实数对(m,n),使f(x-m)+g(x-n)为偶函数?如存在,求出m、n;如不存在,说明理由.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)把f(x)和g(x)代入方程f(x)=g(x),因式分解,转化为一元二次方程根的问题,求得b的取值范围.
(2)根据偶函数的性质得到关于m,n的方程组,解得即可.
(2)根据偶函数的性质得到关于m,n的方程组,解得即可.
解答:
解:(1)由f(x)=g(x)可得x2(x2-4x+4-b)=0,
由题意知此方程有三个不相等的实数根,
此时x=0为方程的一实数根,则方程x2-4x+4-b=0应有两个不相等的非零实根,
∴△>0,且4-b≠0,
即(-4)2-4(4-b)>0且b≠4,
解得b>0且b≠4,
∴所求b的取值范围是(0,4)∪(4,+∞).
(2)解:f(x-m)+g(x-n)=x4-4x3(m+1)+2x2(3m2+6m-2+
)-2x(2m3+6m2+4m-bn)+m4+4m2+bn2-2为偶函数,
∴
解得
由(2)知b≠0
∴m=-1,n=0.
由题意知此方程有三个不相等的实数根,
此时x=0为方程的一实数根,则方程x2-4x+4-b=0应有两个不相等的非零实根,
∴△>0,且4-b≠0,
即(-4)2-4(4-b)>0且b≠4,
解得b>0且b≠4,
∴所求b的取值范围是(0,4)∪(4,+∞).
(2)解:f(x-m)+g(x-n)=x4-4x3(m+1)+2x2(3m2+6m-2+
| b |
| 2 |
∴
|
解得
|
由(2)知b≠0
∴m=-1,n=0.
点评:以本题主要考查了偶函数的性质及一元二次方程根的存在性的判定,体现了数形结合的思想方法,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
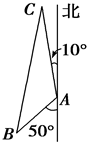 我舰在岛A南偏西50°相距12海里的B处发现敌舰正从岛A沿北偏西10°的方向以每小时10海里的速度航行,若我舰要用2小时追上敌舰,求我舰航行速度.
我舰在岛A南偏西50°相距12海里的B处发现敌舰正从岛A沿北偏西10°的方向以每小时10海里的速度航行,若我舰要用2小时追上敌舰,求我舰航行速度.