题目内容

6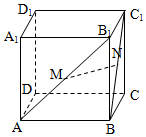．在棱长为1的正方体ABCD-A1B1C1D1中，M、N分别是AB1、BC1的中点．
（Ⅰ）求证：直线MN∥平面ABCD．
（Ⅱ）求四面体B1A1BC1的体积．

分析 （Ⅰ）连结B1C、AC，则N也是B1C的中点，证明MN∥AC，即可证明：直线MN∥平面ABCD．
（Ⅱ）利用等体积方法求四面体B1A1BC1的体积．

解答 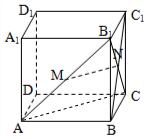（Ⅰ）证明：连结B1C、AC，则N也是B1C的中点
∴MN是△B1AC的中位线，即有MN∥AC…（3分）
∵MN?平面ABCD，AC?平面ABCD
∴MN∥平面ABCD…（5分）
（Ⅱ）解：∵${V_{{A_1}-{B_{1B{C_1}}}}}=\frac{1}{3}×（\frac{1}{2}×1×1）×1=\frac{1}{6}$（7分）
又${V_{{B_1}-{A_{1B{C_1}}}}}={V_{{A_1}-{B_{1B{C_1}}}}}$，∴${V_{{B_1}-{A_{1B{C_1}}}}}=\frac{1}{6}$…（10分）

点评 本题考查线面平行的证明，考查体积公式的运用，属于中档题．

练习册系列答案
相关题目
2．在△ABC中，A、B、C的对边分别为a、b、c，若B=$\frac{π}{3}$，b=6，sinA-2sinC=0，则a=（　　）
A．3B．2$\sqrt{3}$C．4$\sqrt{3}$D．12
3．已知f（x）=lnx-x+m（m为常数）．
（1）求f（x）的极值；
（2）设m＞1，记f（x+m）=g（x），已知x1，x2为函数g（x）是两个零点，求证：x1+x2＜0．
14．已知圆C：x2+（y-1）2=5，直线l：mx-y+2-m=0．
（Ⅰ）求证：对m∈R，直线l与圆C总有两个不同的交点A，B；
（Ⅱ）若∠ACB=120°，求m的值；
（Ⅲ）当|AB|取最小值时，求直线l的方程．
1．设变量x，y满足$\left\{\begin{array}{l}{x-y≤10}\\{0≤x+y≤20}\\{0≤y≤15}\end{array}\right.$，则2x+3y的最大值为55．
11．复数$\frac{（1+i）（3+4i）}{i}$等于（　　）
A．7+iB．7-iC．7+7iD．-7+7i
18．已知数列{an}的前n项和Sn=n2+pn，且a2，a5，a10成等比数列．
（1）求数列{an}的通项公式；
（2）若bn=1+$\frac{5}{{a}_{n}•{a}_{n+1}}$，求数列{bn}的前n项和Tn．
15．已知函数$f（x）=mx-\frac{m-1+2e}{x}-lnx$，m∈R，函数$g（x）=\frac{1}{xcosθ}+lnx$在[1，+∞）上为增函数，且θ∈$（{-\frac{π}{2}，\frac{π}{2}}）$．
（Ⅰ）当m=0时，求函数f（x）的单调区间和极值；
（Ⅱ）求θ的值；
（Ⅲ）若在[1，e]上至少存在一个x0，使得f（x0）＞g（x0）成立，求m的取值范围．
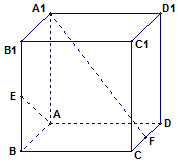16．如图，正方体ABCD-A1B1C1D1的棱长为1，E、F分别是BB1和CD的中点．
（Ⅰ）求AE与A1F所成角的大小；
（Ⅱ）求AE与平面ABCD所成角的正切值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网