题目内容
2．在△ABC中，A、B、C的对边分别为a、b、c，若B=$\frac{π}{3}$，b=6，sinA-2sinC=0，则a=（ ）| A． | 3 | B． | 2$\sqrt{3}$ | C． | 4$\sqrt{3}$ | D． | 12 |
分析 由已知及正弦定理可得：c=$\frac{1}{2}a$，进而利用余弦定理即可求得a的值．
解答 解：∵sinA-2sinC=0，
∴由正弦定理可得：c=$\frac{1}{2}a$，
∵B=$\frac{π}{3}$，b=6，
∴由余弦定理b2=a2+c2-2accosB，可得：62=a2+（$\frac{1}{2}$a）2-2a$•\frac{a}{2}•\frac{1}{2}$，整理可得：a=4$\sqrt{3}$，或-4$\sqrt{3}$（舍去）．
故选：C．
点评 本题主要考查了正弦定理，余弦定理在解三角形中的应用，考查了计算能力和转化思想，属于基础题．
练习册系列答案
教材全解字词句篇系列答案
相关题目
12．已知复数z1=3+4i，z2=t-i，且z1•$\overline{{z}_{2}}$是实数，则实数t=（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | -$\frac{4}{3}$ | D． | -$\frac{3}{4}$ |
10．已知抛物线x2=2y的焦点与椭圆$\frac{{y}^{2}}{m}$+$\frac{{x}^{2}}{2}$=1的一个焦点重合，则m=（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | $\frac{9}{4}$ |
17．下列说法正确的是（ ）
| A． | ?x，y∈R，若x+y≠0，则x≠1且y≠-1 | |
| B． | a∈R，“$\frac{1}{a}$＜1“是“a＞1“的必要不充分条件 | |
| C． | 命题“?x∈R，使得x2+2x+3＜0”的否定是“?x∈R，都有x2+2x+3＞0” | |
| D． | “若am2＜bm2，则a＜b”的逆命题为真命题 |
7．同时具有性质：①图象的相邻两条对称轴间的距离是$\frac{π}{2}$；②在[-$\frac{π}{6}$，$\frac{π}{3}$]上是增函数的一个函数为（ ）
| A． | y=sin（$\frac{x}{2}$+$\frac{π}{6}$） | B． | y=cos（2x+$\frac{π}{3}$） | C． | y=sin（2x-$\frac{π}{6}$） | D． | y=cos（$\frac{x}{2}$-$\frac{π}{6}$） |
14．已知A是抛物线M：y2=2px（p＞0）与圆C在第一象限的公共点，其中圆心C（0，4），点A到M的焦点F的距离与C的半径相等，M上一动点到其准线与到点C的距离之和的最小值等于C的直径，O为坐标原点，则直线OA被圆C所截得的弦长为（ ）
| A． | 2 | B． | 2$\sqrt{3}$ | C． | $\frac{7\sqrt{2}}{6}$ | D． | $\frac{7\sqrt{2}}{3}$ |
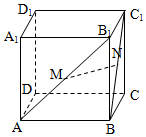在棱长为1的正方体ABCD-A1B1C1D1中，M、N分别是AB1、BC1的中点．