题目内容
13.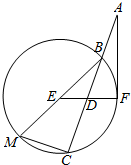 如图,AF是圆E切线,F是切点,割线ABC,BM是圆E的直径,EF交AC于D,$AB=\frac{1}{3}AC$,∠EBC=30°,MC=2.
如图,AF是圆E切线,F是切点,割线ABC,BM是圆E的直径,EF交AC于D,$AB=\frac{1}{3}AC$,∠EBC=30°,MC=2.(Ⅰ)求线段AF的长;
(Ⅱ)求证:AD=3ED.
分析 (Ⅰ)推导出∠BCM=90°,BC=2$\sqrt{3}$,AC=3$\sqrt{3}$,由切割线定理能求出AF.
(Ⅱ)过E作EH⊥BC于H,则△EDH∽△ADF,由此能证明AD=3ED.
解答 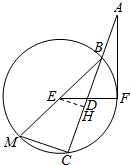 (本题满分10分)选修4-1:几何证明选讲
(本题满分10分)选修4-1:几何证明选讲
解:(Ⅰ)∵BM是圆E直径,∴∠BCM=90°,…(1分)
又MC=2,∠EBC=30°,∴BC=2$\sqrt{3}$,…(2分)
又AB=$\frac{1}{3}$AC,∴AB=$\frac{1}{2}BC=\sqrt{3}$,∴AC=3$\sqrt{3}$,…(3分)
根据切割线定理得:$A{F}^{2}=AB•AC=\sqrt{3}×3\sqrt{3}$=9,…(4分)
解得AF=3.…(5分)
证明:(Ⅱ)过E作EH⊥BC于H,…(6分)
则△EDH∽△ADF,…(7分)
从而有$\frac{ED}{AD}=\frac{EH}{AF}$,…(8分)
又由题意知CH=$\frac{1}{2}$BC=$\sqrt{3}$,EB=2,
∴EH=1,…(9分)
∴$\frac{ED}{AD}=\frac{1}{3}$,即AD=3ED.…(10分)
点评 本题考查线段长的求法,考查两线段等量关系的证明,是中档题,解题时要认真审题,注意切割线定理的合理运用.

练习册系列答案
相关题目
2.已知等边△ABC的边长为2,若$\overrightarrow{BC}$=3$\overrightarrow{BE}$,$\overrightarrow{AD}$=$\overrightarrow{DC}$,则$\overrightarrow{BD}$•$\overrightarrow{AE}$等于( )
| A. | -2 | B. | -$\frac{10}{3}$ | C. | 2 | D. | $\frac{10}{3}$ |
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AB⊥AC,AC⊥PB,点E为PD上一点,AE=$\frac{1}{2}$PD,PB∥平面AEC,求证:PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AB⊥AC,AC⊥PB,点E为PD上一点,AE=$\frac{1}{2}$PD,PB∥平面AEC,求证:PA⊥平面ABCD.