题目内容
2.曲线y=4x-x3在点(-1,-3)处的切线的倾斜角是$\frac{π}{4}$.分析 求函数的导数,利用导数的几何意义进行求解即可.
解答 解:函数的导数f′(x)=4-3x2,
则函数点(-1,-3)处的切线斜率k=f′(-1)=4-3=1,
即tanα=1,则α=$\frac{π}{4}$,
即切线的倾斜角为$\frac{π}{4}$,
故答案为:$\frac{π}{4}$
点评 本题主要考查导数的几何意义的应用,根据导数的几何意义是解决本题的关键.比较基础.

练习册系列答案
相关题目
10.计算log62+log63=( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
17.设x1,x2是方程x2+px+4=0的两个不相等的实数根,则( )
| A. | |x1|>2,|x2|>2 | B. | |x1+x2|>4 | C. | |x1|=4,|x2|=1 | D. | |x1+x2|<4 |
7.五名学生站成一排,则甲乙相邻的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{9}{10}$ |
11.已知函数y=x2-4ax在[1,3]上是增函数,则实数a的取值范围是( )
| A. | (-∞,1] | B. | (-∞,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,$\frac{3}{2}$] | D. | [$\frac{3}{2}$,+∞) |
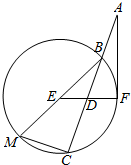 如图,AF是圆E切线,F是切点,割线ABC,BM是圆E的直径,EF交AC于D,$AB=\frac{1}{3}AC$,∠EBC=30°,MC=2.
如图,AF是圆E切线,F是切点,割线ABC,BM是圆E的直径,EF交AC于D,$AB=\frac{1}{3}AC$,∠EBC=30°,MC=2.