题目内容
1.已知a是实数,则函数f(x)=1+asinax的图象不可能是( )| A. | 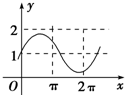 | B. | 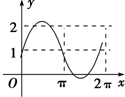 | C. | 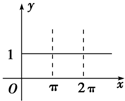 | D. | 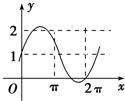 |
分析 根据当a=0时,y=1,可判断图象哪个符合,
当a≠0时,f(x) 周期为$\frac{2π}{a}$,振幅a,
分类讨论a>1时,T<2π;0<a≤1,T≥2π利用所给图象判断即可得出正确答案.
解答 解:∵函数f(x)=1+asinax
(1)当a=0时,y=1,函数图象为:C
故C正确
(2)当a≠0时,f(x)=1+asinax 周期为T=$\frac{2π}{a}$,振幅为a
若a>1时,振幅为a>1,T<2π,
当0<a≤1,T≥2π.
∵D选项的图象,振幅与周期的范围矛盾
故D错误,
故选:D
点评 本题考察了三角函数的图象和性质,分类讨论的思想,属于中档题,关键是确定分类的标准,和函数图象的对应.

练习册系列答案
相关题目
7.已知F1,F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)左右两焦点,以F1为圆心的圆恰经过双曲线的中心,过F2作⊙F1的切线,切点为P,若点P恰在双曲线一条渐近线上,则此双曲线的离心率为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$+1 | D. | 4 |
10.计算log62+log63=( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
11.已知函数y=x2-4ax在[1,3]上是增函数,则实数a的取值范围是( )
| A. | (-∞,1] | B. | (-∞,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,$\frac{3}{2}$] | D. | [$\frac{3}{2}$,+∞) |
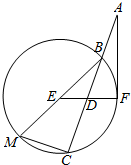 如图,AF是圆E切线,F是切点,割线ABC,BM是圆E的直径,EF交AC于D,$AB=\frac{1}{3}AC$,∠EBC=30°,MC=2.
如图,AF是圆E切线,F是切点,割线ABC,BM是圆E的直径,EF交AC于D,$AB=\frac{1}{3}AC$,∠EBC=30°,MC=2.