题目内容
2.已知等边△ABC的边长为2,若$\overrightarrow{BC}$=3$\overrightarrow{BE}$,$\overrightarrow{AD}$=$\overrightarrow{DC}$,则$\overrightarrow{BD}$•$\overrightarrow{AE}$等于( )| A. | -2 | B. | -$\frac{10}{3}$ | C. | 2 | D. | $\frac{10}{3}$ |
分析 根据题意得出$\overrightarrow{BD}$=$\frac{1}{2}$($\overrightarrow{BA}$+$\overrightarrow{BC}$),$\overrightarrow{AE}$=$\frac{1}{3}$$\overrightarrow{BC}$-$\overrightarrow{BA}$,运用数量积求解即可.
解答 解:等边△ABC的边长为2,$\overrightarrow{BC}$=3$\overrightarrow{BE}$,$\overrightarrow{AD}$=$\overrightarrow{DC}$,
∴$\overrightarrow{BD}$=$\frac{1}{2}$($\overrightarrow{BA}$+$\overrightarrow{BC}$),$\overrightarrow{AE}$=$\frac{1}{3}$$\overrightarrow{BC}$-$\overrightarrow{BA}$,
∴$\overrightarrow{BD}$•$\overrightarrow{AE}$=$\frac{1}{2}$($\frac{1}{3}$${\overrightarrow{BC}}^{2}$-${\overrightarrow{BA}}^{2}$-$\frac{2}{3}\overrightarrow{BC}•\overrightarrow{BA}$),
=$\frac{1}{2}$×($\frac{1}{3}$×4-4-$\frac{2}{3}$×2×2×$\frac{1}{2}$),
=-2.
故选A
点评 本题考查了平面向量的运算,数量积的求解,属于中档题,关键是分解向量.

| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
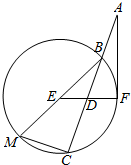 如图,AF是圆E切线,F是切点,割线ABC,BM是圆E的直径,EF交AC于D,$AB=\frac{1}{3}AC$,∠EBC=30°,MC=2.
如图,AF是圆E切线,F是切点,割线ABC,BM是圆E的直径,EF交AC于D,$AB=\frac{1}{3}AC$,∠EBC=30°,MC=2.