题目内容
1. 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AB⊥AC,AC⊥PB,点E为PD上一点,AE=$\frac{1}{2}$PD,PB∥平面AEC,求证:PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AB⊥AC,AC⊥PB,点E为PD上一点,AE=$\frac{1}{2}$PD,PB∥平面AEC,求证:PA⊥平面ABCD.
分析 由AB⊥AC,AC⊥PB,即可证AC⊥AP,连接BD,交AC与点O,连接OE,有DO=OB,由PB∥平面AEC,可证PB∥OE,从而可得PE=ED,结合AE=$\frac{1}{2}$PD,可得点P,A,D三点共圆,可得:PA⊥AD,即可证明PA⊥平面ABCD.
解答 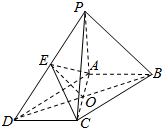 证明:∵AB⊥AC,AC⊥PB,AB∩PB=B,
证明:∵AB⊥AC,AC⊥PB,AB∩PB=B,
∴AC⊥平面ABP,
∵PA?平面ABP
∴AC⊥AP,
如图,连接BD,交AC与点O,连接OE,
∵底面ABCD是平行四边形,
∴DO=OB,
∵PB∥平面AEC,PB?平面PAB,平面PAB∩平面AEC=OE,
∴PB∥OE,
∴PE=ED,
∵AE=$\frac{1}{2}$PD,
∴PE=ED=AE,即:点P,A,D三点共圆,可得:PA⊥AD,
又∵AC∩AD=A,底面ABCD是平行四边形,
∴PA⊥平面ABCD.
点评 本题主要考查了直线与平面垂直的判定,直线与平面平行的性质的应用,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
11.若直线y=kx-2与抛物线y2=8x交于A,B两个不同的点,且AB的中点的横坐标为2,则k=( )
| A. | 2 | B. | -1 | C. | 2或-1 | D. | 1±$\sqrt{5}$ |
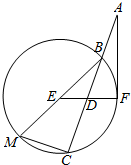 如图,AF是圆E切线,F是切点,割线ABC,BM是圆E的直径,EF交AC于D,$AB=\frac{1}{3}AC$,∠EBC=30°,MC=2.
如图,AF是圆E切线,F是切点,割线ABC,BM是圆E的直径,EF交AC于D,$AB=\frac{1}{3}AC$,∠EBC=30°,MC=2.