题目内容
8.一个袋中有红、白两种球各若干个,现从中一次性摸出两个球,假设摸出的两个球至少有一个红球的概率为$\frac{7}{15}$,至少一个白球的概率为$\frac{13}{15}$,求摸出的两个球恰好红球白球各一个的概率.分析 设摸到的两个球均为红色的事件为A,一红一白的事件为B,均为白球的事件为C.A、B、C为互斥事件,由此列出方程组能求出两个球恰好红球白球各一个的概率.
解答 15.解:设摸到的两个球均为红色的事件为A,一红一白的事件为B,均为白球的事件为C.
A、B、C为互斥事件,
依题意:$\left\{\begin{array}{l}P(A+B)=\frac{7}{15}\\ P(B+C)=\frac{13}{15},P(A+B+C)=1\end{array}$,
$\left\{\begin{array}{l}P(A)+P(B)=\frac{7}{15}\\ P(B)+P(C)=\frac{13}{15},P(A)+P(B)+P(C)=1\end{array}$,
P(B)=$\frac{1}{3}$.
∴两个球恰好红球白球各一个的概率为$\frac{1}{3}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意互斥事件概率加法公式的合理运用.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
17.在△ABC中,内角A,B,C的对边分别为a,b,c,若cosA=$\frac{7}{8}$,c-a=2,b=3,则a等于( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
17.设x1,x2是方程x2+px+4=0的两个不相等的实数根,则( )
| A. | |x1|>2,|x2|>2 | B. | |x1+x2|>4 | C. | |x1|=4,|x2|=1 | D. | |x1+x2|<4 |
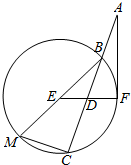 如图,AF是圆E切线,F是切点,割线ABC,BM是圆E的直径,EF交AC于D,$AB=\frac{1}{3}AC$,∠EBC=30°,MC=2.
如图,AF是圆E切线,F是切点,割线ABC,BM是圆E的直径,EF交AC于D,$AB=\frac{1}{3}AC$,∠EBC=30°,MC=2.