题目内容
3.设等比数列{an}的前n项和为Sn,已知8a1,3a2,2a2成等差数列,S4=5.(1)求数列{an}的通项公式;
(2)设数列{bn}的首项为2,公差为-a1的等差数列,其前n项和为Tn,求满足Tn-1>0的最大正整数n.
分析 (1)设等比数列{an}的公比为q,运用等差数列的中项的性质,可得q=2,再由等比数列的求和公式,可得首项,进而得到所求通项公式;
(2)运用等差数列的通项公式和求和公式,结合二次不等式的解法,即可得到所求的最大值.
解答 解:(1)设等比数列{an}的公比为q,
由8a1,3a2,2a2成等差数列,可得
6a2=8a1+2a2,即为a2=2a1,
即有q=2,
由S4=5,可得$\frac{{a}_{1}(1-{q}^{4})}{1-q}$=5,
代入q=2,解得a1=$\frac{1}{3}$,
则an=a1qn-1=$\frac{1}{3}$•2n-1;
(2)由题意可得bn=2+(n-1)•(-$\frac{1}{3}$)=$\frac{7-n}{3}$,
前n项和为Tn=$\frac{1}{2}$n(2+$\frac{7-n}{3}$)=$\frac{n(13-n)}{6}$,
由Tn-1>0,即为$\frac{(n-1)(14-n)}{6}$>0,解得1<n<14.
即有满足Tn-1>0的最大正整数n为13.
点评 本题考查等差数列和等比数列的通项公式和求和公式的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
11.已知函数y=x2-4ax在[1,3]上是增函数,则实数a的取值范围是( )
| A. | (-∞,1] | B. | (-∞,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,$\frac{3}{2}$] | D. | [$\frac{3}{2}$,+∞) |
8.“a=1”是“两直线y=ax-2和3x-(a+2)y+2=0互相平行”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
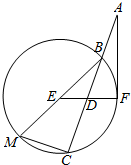 如图,AF是圆E切线,F是切点,割线ABC,BM是圆E的直径,EF交AC于D,$AB=\frac{1}{3}AC$,∠EBC=30°,MC=2.
如图,AF是圆E切线,F是切点,割线ABC,BM是圆E的直径,EF交AC于D,$AB=\frac{1}{3}AC$,∠EBC=30°,MC=2.