题目内容
14．如图，由函数f（x）=x2-x的图象与x轴、直线x=2围成的阴影部分的面积为1．
分析 首先利用定积分表示阴影部分的面积，然后计算定积分即可．
解答 解：由函数f（x）=x2-x的图象与x轴、直线x=2围成的阴影部分的面积为
${∫}_{0}^{1}（x-{x}^{2}）dx+{∫}_{1}^{2}（{x}^{2}-x）dx$=$（\frac{1}{2}{x}^{2}-\frac{1}{3}{x}^{3}）{|}_{0}^{1}+（\frac{1}{3}{x}^{3}-\frac{1}{2}{x}^{2}）{|}_{1}^{2}$=1；
故答案为：1．
点评 本题考查了定积分的运用；关键是明确定积分的几何意义，正确利用定积分表示阴影部分的面积．
练习册系列答案
相关题目
5．
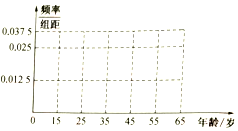随着生活水平的提高，人们对空气质量的要求越来越高，某机构为了解公众对“车辆限行”的态度，随机抽查40人，并将调查情况进行整理后制成如表：
（1）完成被调查人员年龄的频率分布直方图，并求被调査人员中持赞成态度人员的平均年龄约为多少岁？
（2）若从年龄在[15，25），[45，55）的被调查人员中各随机选取1人进行调查．请写出所有的基本亊件，并求选取2人中恰有1人持不赞成态度的概率．
随着生活水平的提高，人们对空气质量的要求越来越高，某机构为了解公众对“车辆限行”的态度，随机抽查40人，并将调查情况进行整理后制成如表：| 年龄（岁） | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） |
| 频数 | 5 | 10 | 10 | 5 | 10 |
| 赞成人数 | 4 | 6 | 8 | 4 | 9 |
（2）若从年龄在[15，25），[45，55）的被调查人员中各随机选取1人进行调查．请写出所有的基本亊件，并求选取2人中恰有1人持不赞成态度的概率．
2．函数f（x）=Asin（ωx+φ）的部分图象如图所示，若f（4）=-f（6）=-1，且$f（\frac{1}{2}）=0$，则f（2017）=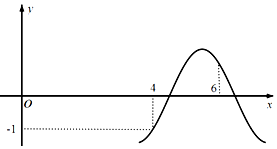
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | 1 | D． | $\frac{\sqrt{3}}{2}$ |
9．在复平面上，复数z=（-2+i）i5的对应点所在象限是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |