题目内容
9.在复平面上,复数z=(-2+i)i5的对应点所在象限是( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数的运算法则、几何意义即可得出.
解答 解:复数z=(-2+i)i5=i(-2+i)=-1-2i对应点(-1,-2)所在象限是第三象限.
故选:C.
点评 本题考查了复数的运算法则、几何意义,考查了计算能力,属于基础题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
19.为了得到函数$y=3sin(x+\frac{π}{3})$的图象,只需将函数y=3sin(x-$\frac{π}{3}$)的图象( )
| A. | 向右平移$\frac{π}{3}$个单位长度 | B. | 向左平移$\frac{π}{3}$个单位长度 | ||
| C. | 向右平移$\frac{2π}{3}$个单位长度 | D. | 向左平移$\frac{2π}{3}$个单位长度 |
20.佳佳同学在8次测试中,数学成绩的茎叶图如图,则这8次成绩的中位数是( )
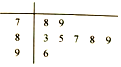

| A. | 86 | B. | 87 | C. | 87.5 | D. | 88.5 |
17. 如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )
如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )
 如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )
如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )| A. | $\sqrt{6}-1$ | B. | $\sqrt{6}$ | C. | $\sqrt{6}+1$ | D. | $2\sqrt{3}$ |
1.复数$\frac{2}{1-i}$=( )
| A. | $\sqrt{2}$+$\sqrt{2}$i | B. | $\frac{{\sqrt{2}}}{2}$+$\frac{{\sqrt{2}}}{2}$i | C. | 1-i | D. | 1+i |
18.已知集合A={x|x2-16<0},B={-4,-2,0,1},则( )
| A. | B⊆A | B. | A∩B=∅ | C. | A∩B={0,1} | D. | A∩B={-2,0,1} |
19.函数y=sinx•cosx的导数是( )
| A. | cosx•sinx | B. | cos2x+sin2x | C. | 2cosx•sinx | D. | cos2x-sin2x |
