题目内容
5. 随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查40人,并将调查情况进行整理后制成如表:
随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查40人,并将调查情况进行整理后制成如表:| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 5 | 10 | 10 | 5 | 10 |
| 赞成人数 | 4 | 6 | 8 | 4 | 9 |
(2)若从年龄在[15,25),[45,55)的被调查人员中各随机选取1人进行调查.请写出所有的基本亊件,并求选取2人中恰有1人持不赞成态度的概率.
分析 (1)由频率数分布列能求出被调查人员年龄的频率分布直方图,由频率分布直方图能求出被调查人员持赞成态度人的平均年龄.
(2)设[15,25)中赞成的4人分别为A1,A2,A3,A4,不赞成的1人为a,[45,55)中赞成的4人分别为B1,B2,B3,B4,不赞成的1人为b.由此利用列举法能求出恰有1人持不赞成态度的概率.
解答 解:(1)被调查人员年龄的频率分布直方图如图所示: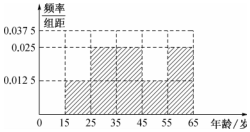
被调查人员持赞成态度人的平均年龄约为:
$\overline x=\frac{4×20+6×30+8×40+4×50+9×60}{4+6+8+4+9}≈42.6$(岁).
(2)设[15,25)中赞成的4人分别为A1,A2,A3,A4,不赞成的1人为a,
[45,55)中赞成的4人分别为B1,B2,B3,B4,不赞成的1人为b.基本事件为:
(A1,B1),(A1,B2),(A1,B3),(A1,B4),(A1,b),(A2,B1),
(A2,B2),(A2,B3),(A2,B4),(A2,b),(A3,B1),(A3,B2),
(A3,B3),(A3,B4),(A3,b),(A4,B1),(A4,B2),(A4,B3),
(A4,B4),(A4,b),(a,B1),(a,B2),(a,B3),(a,B4),(a,b),
基本事件共有5×5=25个,
其中恰有1人持不赞成态度的基本事件为1+1+1+1+4=8个.
据古典概型知:恰有1人持不赞成态度的概率$P=\frac{8}{25}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
13.若对?x∈[0,+∞),y∈[0,+∞),不等式ex+y-2+ex-y-2+2-4ax≥0恒成立,则实数a取值范围是( )
| A. | $({-∞,\frac{1}{4}}]$ | B. | $[{\frac{1}{4},+∞})$ | C. | $[{\frac{1}{2},+∞})$ | D. | $({-∞,\frac{1}{2}}]$ |
20.佳佳同学在8次测试中,数学成绩的茎叶图如图,则这8次成绩的中位数是( )
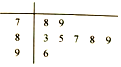

| A. | 86 | B. | 87 | C. | 87.5 | D. | 88.5 |
10.5支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是$\frac{1}{2}$.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:p1:恰有四支球队并列第一名为不可能事件;p2:有可能出现恰有两支球队并列第一名;p3:每支球队都既有胜又有败的概率为$\frac{17}{32}$;p4:五支球队成绩并列第一名的概率为$\frac{3}{32}$.其中真命题是( )
| A. | p1,p2,p3 | B. | p1,p2,p4 | C. | p1,p3,p4 | D. | p2,p3,p4 |
17. 如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )
如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )
 如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )
如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )| A. | $\sqrt{6}-1$ | B. | $\sqrt{6}$ | C. | $\sqrt{6}+1$ | D. | $2\sqrt{3}$ |
15.数列1,3,5,7,9,…的通项公式是( )
| A. | n-1(n∈N+) | B. | 2n-1(n∈N+) | C. | n(n∈N+) | D. | 3n-3(n∈N+) |
