题目内容
2.函数f(x)=Asin(ωx+φ)的部分图象如图所示,若f(4)=-f(6)=-1,且$f(\frac{1}{2})=0$,则f(2017)=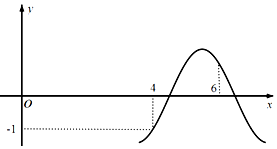
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
分析 根据图象经过的点以及自变量4,6的函数值关系分别求出ω,φ,A,然后求值.
解答 解:因为f(x)=Asin(ωx+φ)的部分图象,f(4)=-f(6)=-1,得到周期为T=2(6-4)=4,所以$ω=\frac{2π}{4}=\frac{π}{2}$,且$f(\frac{1}{2})=0$,所以Asin($\frac{π}{4}$+φ)=0,得到φ=$-\frac{π}{4}$,
又f(4)=-1,所以Asin(2$π-\frac{π}{4}$)=-1,解得A=$\sqrt{2}$,所以f(x)=$\sqrt{2}$sin($\frac{π}{2}x-\frac{π}{4}$)
所以f(2017)=f(504×4+1)=f(1)=$\sqrt{2}$sin($\frac{π}{2}-\frac{π}{4}$)=$\sqrt{2}×\frac{\sqrt{2}}{2}$=1;
故选C.
点评 本题考查由y=Asin(ωx+φ)的部分图象确定解析式,考查数形结合思想,属中档题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
12.设二次函数f(x)=x2+ax+b,若对任意的实数a,都存在实数$x∈[{\frac{1}{2},2}]$,使得不等式|f(x)|≥x成立,则实数b的取值范围是( )
| A. | $({-∞,-\frac{1}{3}}]∪[{2,+∞}]$ | B. | $({-∞,-\frac{1}{3}}]∪[{\frac{1}{4},+∞})$ | C. | $({-∞,\frac{1}{4}}]∪[{\frac{9}{4},+∞})$ | D. | $({-∞,-\frac{1}{3}}]∪[{\frac{9}{4},+∞})$ |
13.若对?x∈[0,+∞),y∈[0,+∞),不等式ex+y-2+ex-y-2+2-4ax≥0恒成立,则实数a取值范围是( )
| A. | $({-∞,\frac{1}{4}}]$ | B. | $[{\frac{1}{4},+∞})$ | C. | $[{\frac{1}{2},+∞})$ | D. | $({-∞,\frac{1}{2}}]$ |
10.5支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是$\frac{1}{2}$.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:p1:恰有四支球队并列第一名为不可能事件;p2:有可能出现恰有两支球队并列第一名;p3:每支球队都既有胜又有败的概率为$\frac{17}{32}$;p4:五支球队成绩并列第一名的概率为$\frac{3}{32}$.其中真命题是( )
| A. | p1,p2,p3 | B. | p1,p2,p4 | C. | p1,p3,p4 | D. | p2,p3,p4 |
17. 如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )
如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )
 如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )
如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )| A. | $\sqrt{6}-1$ | B. | $\sqrt{6}$ | C. | $\sqrt{6}+1$ | D. | $2\sqrt{3}$ |
12.$\int_0^5{(2x-4)dx}$=( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
