题目内容
已知f（x）=（x-2）2，x∈[-1，3]，函数f（x+1）得单调递减区间为 ．
考点：函数单调性的判断与证明
专题：计算题,函数的性质及应用
分析：根据f（x）=（x-2）2，x∈[-1，3]，用x+1替代x，求出函数f（x+1）的解析式．再利用二次函数y=x2-2x+1的图象是抛物线，开口向上，对称轴为 x=1，可得它在x∈[-2，2]范围内的减区间．
解答：
解：由于f（x）=（x-2）2，x∈[-1，3]，
则函数f（x+1）=[（x+1）-2]2=（x-1）2=x2-2x+1，x∈[-2，2]，
故函数的单调递减区间为[-2，1]．
故答案为：[-2，1]
则函数f（x+1）=[（x+1）-2]2=（x-1）2=x2-2x+1，x∈[-2，2]，
故函数的单调递减区间为[-2，1]．
故答案为：[-2，1]
点评：本题主要考查二次函数的性质：单调性及应用，考查运算能力，属于基础题和易错题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
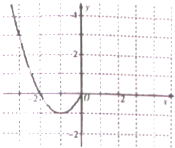已知函数f（x）是定义在R上的偶函数，且当x≤0时，f（x）图象是抛物线的一部分（如图所示）．
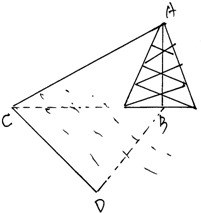如图所示，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C与D，现测得∠BCD=α，∠BDC=β，CD=s，并在点C测得塔顶A的仰角为θ，则塔高AB=