题目内容
已知空间三点的坐标为A（1，5，-2），B（2，4，1），C（p，3，q+2），若A、B、C三点共线，则p+q=（ ）
| A、2 | B、3 | C、4 | D、5 |
考点：共线向量与共面向量
专题：空间向量及应用
分析：利用向量共线定理即可得出．
解答：
解：∵A、B、C三点共线，
∴存在实数λ使得
=λ
，
∴（p-1，-2，q+4）=λ（1，-1，3），
∴
，解得λ=2，p=3，q=2，
∴p+q=5．
故选：D．
∴存在实数λ使得
| AC |
| AB |
∴（p-1，-2，q+4）=λ（1，-1，3），
∴
|
∴p+q=5．
故选：D．
点评：本题考查了向量共线定理，属于基础题．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
函数y=x2-2lnx的单调减区间是（ ）
| A、（-1，1） |
| B、（0，1） |
| C、（-1，0） |
| D、（0，2） |
设复数z=1+
i，则z2-2z等于（ ）
| 2 |
| A、3 i | B、-3 i |
| C、3 | D、-3 |
等差数列{an}中，a1=1，公差d=5，如果an=2006，则序号n等于（ ）
| A、400 | B、401 |
| C、402 | D、403 |
设全集是R，M={0，1，2}，N={1，2，3，4}，则（∁RM）∩N=（ ）
| A、{4} |
| B、{3，4} |
| C、{2，3，4} |
| D、{1，2，3，4} |
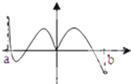函数f（x）的定义域为（a，b），导函数f′（x）在（a，b）内的图象如图所示，则函数f（x）在（a，b）内有极小值点（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
用数学归纳法证明不等式
+
+…+
＞
（n＞2）时的过程中，由n=k到n≠k+1时，不等式的左边（ ）
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
| 13 |
| 24 |
A、增加了一项
| ||||||
B、增加了两项
| ||||||
C、增加了两项
| ||||||
D、增加了一项
|
设过抛物线的焦点F的弦为PQ，则以PQ为直径的圆与抛物线的准线的位置关系（ ）
| A、相交 | B、相切 |
| C、相离 | D、以上答案均有可能 |