题目内容
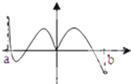函数f（x）的定义域为（a，b），导函数f′（x）在（a，b）内的图象如图所示，则函数f（x）在（a，b）内有极小值点（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
考点：利用导数研究函数的极值
专题：导数的综合应用
分析：直接利用极小值点两侧函数的单调性是先减后增，对应导函数值是先负后正，再结合图象即可求得结论．
解答：
解；因为极小值点两侧函数的单调性是先减后增，对应导函数值是先负后正，
由图得：导函数值先负后正的点只有一个．故函数f（x）在区间（a，b）内极小值点的个数是1．
故选：A．
由图得：导函数值先负后正的点只有一个．故函数f（x）在区间（a，b）内极小值点的个数是1．
故选：A．
点评：本题的易错点在于把原点包含在内，原点处虽然导函数值为0，但在原点两侧，导函数值同号，所以原点不是极值点．
练习册系列答案
相关题目
函数y=log2（|x|+1）的图象大致是（ ）
A、 |
B、 |
C、 |
D、 |
已知f（x）=x3-ax在[1，+∞）上是单调增函数，则a的取值范围是（ ）
| A、（-∞，3] |
| B、（1，3） |
| C、（-∞，3） |
| D、[3，+∞） |
如果等腰三角形的周长是底边长的5倍，那么它的顶角的余弦值是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、
|
抛物线6y2-x=0的准线方程是（ ）
A、x=-
| ||
B、y=
| ||
C、x=-
| ||
D、y=
|
（文）已知函数f（x）是定义在R上且满足f（x）+f（-x）=0，f（x）+f（x+
）=0，且x∈（-
，0）时，f（x）=log
（1-x），则f（2010）+f（2011）=（ ）
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| A、1 | B、2 | C、-1 | D、-2 |
如图，△OAB中，向量| OA |
| a |
| OB |
| b |
| OC |
| 1 |
| 2 |
| OA |
| OD |
| 2 |
| 3 |
| OB |
| OE |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|