题目内容
对于任意的实数a和b,定义一种新的运算“□”:a□b=
,设函数f(x)=(x2-3x)□(x+12)(x∈R),若函数y=f(x)-k的图象与横轴只有一个公共点,则实数k的取值范围是 .
|
考点:函数的零点
专题:计算题,作图题,函数的性质及应用
分析:由题意,化简f(x)=(x2-3x)□(x+12)=
,作出其函数的图象,函数y=f(x)-k的图象与横轴只有一个公共点可化为f(x)与y=k的图象有且只有一个交点,从而求出实数k的取值范围.
|
解答:
解:令x2-3x-(x+12)>0,
则x>6或x<-2,
则f(x)=(x2-3x)□(x+12)
=
,
作出其图象如下图:
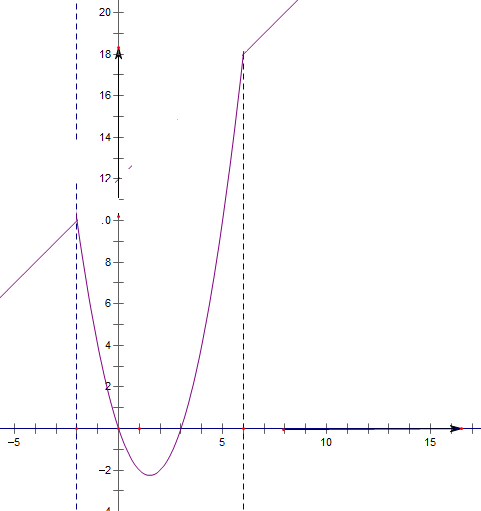
函数y=f(x)-k的图象与横轴只有一个公共点可化为
f(x)与y=k的图象有且只有一个交点,
又∵f(-2)=-2+12=10,
f(
)=-
,
则实数k的取值范围是(-∞,-
)∪(10,+∞);
故答案为:(-∞,-
)∪(10,+∞).
则x>6或x<-2,
则f(x)=(x2-3x)□(x+12)
=
|
作出其图象如下图:

函数y=f(x)-k的图象与横轴只有一个公共点可化为
f(x)与y=k的图象有且只有一个交点,
又∵f(-2)=-2+12=10,
f(
| 3 |
| 2 |
| 9 |
| 4 |
则实数k的取值范围是(-∞,-
| 9 |
| 4 |
故答案为:(-∞,-
| 9 |
| 4 |
点评:本题考查了学生对新知识的接受能力及作图能力,转化能力等,同时考查了数形结合的思想,属于难题.

练习册系列答案
相关题目
| C | 5 12 |
| C | 6 12 |
A、
| ||
B、
| ||
C、
| ||
D、
|
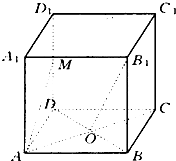 在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,M为D1D的中点.
在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,M为D1D的中点.  如图是一个圆柱被平面所截后余下部分的三视图,尺寸如图所示,则它的体积为
如图是一个圆柱被平面所截后余下部分的三视图,尺寸如图所示,则它的体积为