题目内容
甲、乙两个钢铁厂2010年的年产量均为100万吨,两厂通过革新炼钢技术、改善生产条件等措施,预计从2011年起,在今后10年内,甲厂的年产量每年都比上一年增加10万吨;以2010年为第一年,乙厂第n(n∈N*,n≥2)年的年产量每年都比上一年增加2n-1万吨.
(Ⅰ)“十二•五”期间(即2011年至2015年),甲、乙两个钢铁厂的累计钢产量共多少万吨?
(Ⅱ)若某钢厂的年产量首次超过另一钢厂年产量的2倍,则该钢厂于当年底将另一钢厂兼并,问:在今后10年内,其中一个钢厂能否被另一个钢厂兼并?若能,请推算出哪个钢厂在哪一年底被兼并;若不能,请说明理由.
(Ⅰ)“十二•五”期间(即2011年至2015年),甲、乙两个钢铁厂的累计钢产量共多少万吨?
(Ⅱ)若某钢厂的年产量首次超过另一钢厂年产量的2倍,则该钢厂于当年底将另一钢厂兼并,问:在今后10年内,其中一个钢厂能否被另一个钢厂兼并?若能,请推算出哪个钢厂在哪一年底被兼并;若不能,请说明理由.
考点:函数模型的选择与应用
专题:应用题,等差数列与等比数列
分析:(Ⅰ)由题意知,甲工厂第n年的年产量是构成等差数列,其首项为100,公差是10,而乙工厂的第n年的年产量是一个累加和为bn=100+2+22+23+…+2n-1,数列{an},{bn}的通项公式易得,可求“十二•五”期间(即2011年至2015年),甲、乙两个钢铁厂的累计钢产量;
(Ⅱ)比较两个通项公式,根据情况求出年份即可.
(Ⅱ)比较两个通项公式,根据情况求出年份即可.
解答:
解:(Ⅰ)由题得,甲工厂第n年的年产量是一个等差数列的项,其首项为100,公差是10,∴an=10n+90,
乙工厂的第n年的年产量是一个累加和为bn=100+2+22+23+…+2n-1=2n+98,
∴“十二•五”期间(即2011年至2015年),甲、乙两个钢铁厂的累计钢产量共5×100+
×10+
+490=1002万吨
(Ⅱ)各年的产量如下表
∴2018年底甲工厂将被乙工厂兼并.
乙工厂的第n年的年产量是一个累加和为bn=100+2+22+23+…+2n-1=2n+98,
∴“十二•五”期间(即2011年至2015年),甲、乙两个钢铁厂的累计钢产量共5×100+
| 5×4 |
| 2 |
| 2(1-25) |
| 1-2 |
(Ⅱ)各年的产量如下表
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| an | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 |
| bn | 100 | 102 | 106 | 114 | 130 | 162 | 226 | 354 |
点评:本题考查等差数列与等比数列的综合,考查用数列解决实际问题.由于比较两个工厂的产量时两个函数的形式较特殊,不易求解,故采取了列举法,数据列举时作表格比较简捷.

练习册系列答案
相关题目
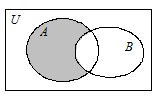
如图所示的韦恩图中,阴影部分对应的集合是( )


| A、A∩B |
| B、∁U(A∩B) |
| C、A∩(∁UB) |
| D、(∁UA)∩B |
 设全集为U=R,集合A={x|(x+3)(x-6)≥0},B={x|log2(x+2)<4}.
设全集为U=R,集合A={x|(x+3)(x-6)≥0},B={x|log2(x+2)<4}.  某简谐运动的图象对应的函数解析式为:y=
某简谐运动的图象对应的函数解析式为:y= 如图:港口A北偏东30°方向的C处有一观测站,港口正东方向的B处有一轮船,测得BC为31n mile,该轮船从B处沿正西方向航行20n mile后到D处,测得CD为21n mile.
如图:港口A北偏东30°方向的C处有一观测站,港口正东方向的B处有一轮船,测得BC为31n mile,该轮船从B处沿正西方向航行20n mile后到D处,测得CD为21n mile.