题目内容
 设全集为U=R,集合A={x|(x+3)(x-6)≥0},B={x|log2(x+2)<4}.
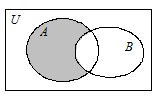
设全集为U=R,集合A={x|(x+3)(x-6)≥0},B={x|log2(x+2)<4}. (1)求集合A,集合B以及如图阴影部分表示的集合;
(2)已知C={x|2a<x<a+1},若C⊆B,求实数a的取值范围.
考点:集合的包含关系判断及应用,Venn图表达集合的关系及运算
专题:集合
分析:弄清两集合中的元素,再进行集合的运算与关系的判断.
解答:
解:(1)集合A=(-∞,-3]∪[6,+∞),B=(-2,14).
图中阴影部分表示的集合为A∩∁UB=(-∞,-3]∪[14,+∞).
(2)当C=∅时,2a≥a+1,解得a≥1;
当C≠∅时,
,解得-1≤a<1.
综上,实数的取值范围是a≥-1.
图中阴影部分表示的集合为A∩∁UB=(-∞,-3]∪[14,+∞).
(2)当C=∅时,2a≥a+1,解得a≥1;
当C≠∅时,
|
综上,实数的取值范围是a≥-1.
点评:本题考查了集合的运算与关系、venn图的相关知识,属基础题,掌握了集合的基础知识,问题即可正确求解.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
若关于x的不等式m≤
x2-2x+3≤n的解集是[m,n](m,n∈R),则n-m的值是( )
| 2 |
| 3 |
| A、3 | ||
| B、2 | ||
C、
| ||
| D、4 |
某商品原价200元,若连续两次涨价10%后出售,则新售价为( )
| A、222元 | B、240元 |
| C、242元 | D、484元 |