题目内容
如图：港口A北偏东30°方向的C处有一观测站，港口正东方向的B处有一轮船，测得BC为31n mile，该轮船从B处沿正西方向航行20n mile后到D处，测得CD为21n mile．（1）求cos∠BDC；
（2）问此时轮船离港口A还有多远？
考点：解三角形的实际应用
专题：应用题,解三角形
分析：（1）在△BDC中，先由余弦定理可得，可求cos∠CDB；
（2）求sin∠CDB，由三角形的内角和定理可得sin∠ACD=sin（∠BDC-60°），再在△ACD中，由正弦定理知，
=
，可求AD．
（2）求sin∠CDB，由三角形的内角和定理可得sin∠ACD=sin（∠BDC-60°），再在△ACD中，由正弦定理知，
| CD |
| sinA |
| AD |
| sin∠ACD |
解答：
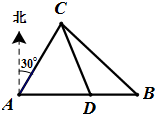解：（1）由条件知∠A=60°，BC=31，BD=20，CD=21，
在△BCD中，由余弦定理，得：cos∠BDC=
=-
；
（2）由（1）知sin∠BDC=
，
∴sin∠ACD=sin（∠BDC-60°）=sin∠BDCcos60°-cos∠BDCsin60°
=
×
-(-
)×
=
．
在△△ACD中，由正弦定理得：
=
，
∴AD=
=15 n mile．
答：此时轮船离港口还有15 n mile．
解：（1）由条件知∠A=60°，BC=31，BD=20，CD=21，在△BCD中，由余弦定理，得：cos∠BDC=
| 202+212-312 |
| 2×21×20 |
| 1 |
| 7 |
（2）由（1）知sin∠BDC=
4
| ||
| 7 |
∴sin∠ACD=sin（∠BDC-60°）=sin∠BDCcos60°-cos∠BDCsin60°
=
4
| ||
| 7 |
| 1 |
| 2 |
| 1 |
| 7 |
| ||
| 2 |
5
| ||
| 14 |
在△△ACD中，由正弦定理得：
| CD |
| sinA |
| AD |
| sin∠ACD |
∴AD=
| CDsin∠ACD |
| sin∠A |
答：此时轮船离港口还有15 n mile．
点评：本题主要考查了正弦定理、余弦定理、两角差的正弦公式及三角形的内角和定理在实际中的应用，解决实际的问题的关键是要把题目中所提供的数据转化成数学图形中的长度（角度），然后根据相应的公式来解决问题．
练习册系列答案
名校课堂系列答案
相关题目
假设你家订了一份早报，送报人可能在早上6：30-7：30之间把报纸送到你家，你父亲离开家去上班的时间在早上7：00-8：00之间，则你父亲离开家前能得到报纸的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD于点E，DA平分∠BDE．