题目内容
设函数f(x)=
x3-ax(a>0),g(x)=bx2+2b-1.
(1)若曲线y=f(x)与y=g(x)在它们的交点(1,c)处有相同的切线,求实数a,b的值;
(2)当a=1,b=0时,求函数h(x)=f(x)+g(x)在区间[t,t+3](t≥-2)上的最小值;
(3)当b=
时,若函数h(x)=f(x)+g(x)在区间(-2,0)内恰有两个零点,求实数a的取值范围.
| 1 |
| 3 |
(1)若曲线y=f(x)与y=g(x)在它们的交点(1,c)处有相同的切线,求实数a,b的值;
(2)当a=1,b=0时,求函数h(x)=f(x)+g(x)在区间[t,t+3](t≥-2)上的最小值;
(3)当b=
| 1-a |
| 2 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:(1)求导数,根据曲线y=f(x)与y=g(x)在它们的交点(1,c)处有相同切线,建立方程,即可求实数a,b的值;
(2)确定函数h(x)的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1),分类讨论,即可得出函数h(x)=f(x)+g(x)在区间[t,t+3]上的最小值;
(3)求导数,确定h(x)在区间(-2,-1)内单调递增,在区间(-1,0)内单调递减,再利用函数h(x)在区间(-2,0)内恰有两个零点,当且仅当
,即可求实数a的取值范围.
(2)确定函数h(x)的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1),分类讨论,即可得出函数h(x)=f(x)+g(x)在区间[t,t+3]上的最小值;
(3)求导数,确定h(x)在区间(-2,-1)内单调递增,在区间(-1,0)内单调递减,再利用函数h(x)在区间(-2,0)内恰有两个零点,当且仅当
|
解答:
解:(1)因为f(x)=
x3-ax(a>0),g(x)=bx2+2b
所以f′(x)=x2-a,g′(x)=2bx,
因为曲线y=f(x)与y=g(x)在它们的交点(1,c)处有相同切线,
所以f(1)=g(1),且f′(1)=g′(1).
即
-a=b+2b-1,且1-a=2b,
解得a=
,b=
;
(2)当a=1,b=0时,h(x)=f(x)+g(x)=
x3-x-1
所以函数h(x)的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1).
由于h(-2)=-
,h(1)=-
,所以h(-2)=h(1).
①当-2≤t<1时,[h(x)]min=h(1)=-
;
③当t≥1时,h(x)在区间[t,t+3]上单调递增,[h(x)]min=h(t)=
t3-t-1;
综上可知,函数h(x)在区间[t,t+3]上的最小值为[h(x)]min=
;
(2)当a=1-2b时,h(x)=
x3+
x2-ax-a(a>0),
所以h′(x)=x2+(1-a)x-a=(x+1)(x-a).
令h′(x)=0,解得x1=-1,x2=a>0.
当x变化时,h′(x),h(x)的变化情况如下表:
所以函数h(x)的单调递增区间为(-∞,-1),(a,+∞),单调递减区间为(-1,a).
故h(x)在区间(-2,-1)内单调递增,在区间(-1,0)内单调递减.
从而函数h(x)在区间(-2,0)内恰有两个零点,当且仅当
即
解得0<a<
.
所以实数a的取值范围是(0,
).
| 1 |
| 3 |
所以f′(x)=x2-a,g′(x)=2bx,
因为曲线y=f(x)与y=g(x)在它们的交点(1,c)处有相同切线,
所以f(1)=g(1),且f′(1)=g′(1).
即
| 1 |
| 3 |
解得a=
| 1 |
| 3 |
| 1 |
| 3 |
(2)当a=1,b=0时,h(x)=f(x)+g(x)=
| 1 |
| 3 |
所以函数h(x)的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1).
由于h(-2)=-
| 5 |
| 3 |
| 5 |
| 3 |
①当-2≤t<1时,[h(x)]min=h(1)=-
| 5 |
| 3 |
③当t≥1时,h(x)在区间[t,t+3]上单调递增,[h(x)]min=h(t)=
| 1 |
| 3 |
综上可知,函数h(x)在区间[t,t+3]上的最小值为[h(x)]min=
|
(2)当a=1-2b时,h(x)=
| 1 |
| 3 |
| 1-a |
| 2 |
所以h′(x)=x2+(1-a)x-a=(x+1)(x-a).
令h′(x)=0,解得x1=-1,x2=a>0.
当x变化时,h′(x),h(x)的变化情况如下表:
| x | (-∞,-1) | -1 | (-1,a) | a | (a,+∞) |
| h′(x) | + | 0 | - | 0 | + |
| h(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
故h(x)在区间(-2,-1)内单调递增,在区间(-1,0)内单调递减.
从而函数h(x)在区间(-2,0)内恰有两个零点,当且仅当
|
即
|
| 1 |
| 3 |
所以实数a的取值范围是(0,
| 1 |
| 3 |
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的最值,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=
,则下列图象错误的是( )
|
A、 y=f(x-1)的图象 |
B、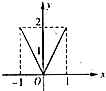 y=f(|x|)的图象 |
C、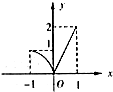 y=f(-x) 的图象 |
D、 y=f(x)的图象 |
假设你家订了一份早报,送报人可能在早上6:30-7:30之间把报纸送到你家,你父亲离开家去上班的时间在早上7:00-8:00之间,则你父亲离开家前能得到报纸的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
某商品原价200元,若连续两次涨价10%后出售,则新售价为( )
| A、222元 | B、240元 |
| C、242元 | D、484元 |