题目内容
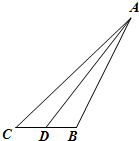如图，在△ABC中，∠C=45°，D为BC中点，BC=2．记锐角∠ADB=α．且满足cosα=-| 7 |
| 25 |
（1）求cos∠CAD；
（2）求BC边上高的值．
考点：解三角形的实际应用
专题：应用题,解三角形
分析：（1）由二倍角公式cos2α=2cos2α-1，可求cosα，根据∠CAD=α-45°，即可求cos∠CAD；
（2）由（1）得，sin∠CAD=sin（α-45°）sinαcos45°-sin45°cosα=
，再由正弦定理
=
，可求AD，从而可由h=ADsin∠ADB求解．
（2）由（1）得，sin∠CAD=sin（α-45°）sinαcos45°-sin45°cosα=
| ||
| 10 |
| CD |
| sin∠CAD |
| AD |
| sin∠C |
解答：
解：（1）∵cos2α=2cos2α-1，∴cos2α=
，
∵α∈（0°，45°），∴cosα=
，
∴sinα=
，
∵∠CAD=α-45°，∴cos∠CAD=cos(α-45°)=
(cosα+sinα)=
．
（2）由（1）得，sin∠CAD=sin（α-45°）=sinαcos45°-sin45°cosα=
，
在△ACD中，由正弦定理得：
=
，
∴AD=
=
=5，
∴高h=ADsin∠ADB=5×
=4．
| 9 |
| 25 |
∵α∈（0°，45°），∴cosα=
| 3 |
| 5 |
∴sinα=
| 4 |
| 5 |
∵∠CAD=α-45°，∴cos∠CAD=cos(α-45°)=
| ||
| 2 |
7
| ||
| 10 |
（2）由（1）得，sin∠CAD=sin（α-45°）=sinαcos45°-sin45°cosα=
| ||
| 10 |
在△ACD中，由正弦定理得：
| CD |
| sin∠CAD |
| AD |
| sin∠C |
∴AD=
| CDsinC |
| sin∠CAD |
1×
| ||||
|
∴高h=ADsin∠ADB=5×
| 4 |
| 5 |
点评：本题主要考查了同角平方关系、和差角公式及正弦定理在求解三角形中的应用，解题的关键是熟练应用基本公式．
练习册系列答案
相关题目
已知如图为函数f（x）=2sin（ωx+φ）（ω＞0，0＜φ＜
某大学生在开学季准备销售一种文具盒进行试创业，在一个开学季内，每售出1盒该产品获利润50元，未售出的产品，每盒亏损30元．根据历史资料，得到开学季市场需求量的频率分布直方图，如图所示．该同学为这个开学季购进了160盒该产品，以x（单位：盒，100≤x≤200）表示这个开学季内的市场需求量，y（单位：元）表示这个开学季内经销该产品的利润．