题目内容
9.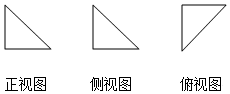 已知一个几何体的正视图、侧视图、俯视图都是腰长为1的等腰直角三角形(如图所示),则该几何体的体积是( )
已知一个几何体的正视图、侧视图、俯视图都是腰长为1的等腰直角三角形(如图所示),则该几何体的体积是( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
分析 由空间几何体的正视图、侧视图、俯视图都为全等的等腰直角三角形结合图象可以判断出此几何体为一个共同一顶点的三个棱两两垂直且此三棱长皆为1的三棱锥,其体积易求.
解答 解:由题设条件知此几何体为一个三棱锥且从同一顶点出发的三个棱两两垂直、长为1.
故以其中两棱组成的三角形为底面,以另一个棱为高,
其体积为$\frac{1}{3}$×$\frac{1}{2}×1×1×1$=$\frac{1}{6}$;
故选D
点评 本题考点是由三视图求几何体的体积,考查三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求体积.

练习册系列答案
相关题目
17.已知函数f(x)=ax3+bx-2,若f(2017)=10,则f(-2017)的值为( )
| A. | -14 | B. | -10 | C. | 10 | D. | 无法确定 |
4.极坐标方程ρ2cos 2θ=1表示的曲线是( )
| A. | 圆 | B. | 双曲线 | C. | 椭圆 | D. | 抛物线 |
14.下列命题中,真命题是( )
| A. | a-b=0的充要条件是$\frac{a}{b}$=1 | B. | ?x∈R,2x>x | ||
| C. | ?x0∈R,|x0|<0 | D. | 若p∧q为假,则p∨q为假 |
1.228与1995的最大公约数是( )
| A. | 57 | B. | 59 | C. | 63 | D. | 67 |
18.设向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为θ,|$\overrightarrow{a}$|≥1,|$\overrightarrow{b}$|≥3,且|$\overrightarrow{a}$|,$\overrightarrow{a}$•$\overrightarrow{b}$,|$\overrightarrow{b}$|成等比数列,则cos2θ的最大值为( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{2}{3}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{1}{4}$ |
19.如果函数f(x)=log3x,那么f($\frac{1}{3}$)等于( )
| A. | -1 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |