题目内容
17．已知函数f（x）=ax3+bx-2，若f（2017）=10，则f（-2017）的值为（ ）| A． | -14 | B． | -10 | C． | 10 | D． | 无法确定 |
分析 根据条件构造奇函数，利用函数奇偶性的性质进行计算即可．
解答 解：∵f（x）=ax3+bx-2，
∴f（x）+2=ax3+bx是奇函数，
则∵f（2017）=10，
∴f（-2017）+2=-[f（2017）+2]=-（10+2）=-12，
则f（-2017）=-12-2=-14，
故选：A
点评 本题主要考查函数值的计算，根据条件构造函数，利用函数的奇偶性是解决本题的关键．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
8．已知实数x，y满足方程x2+y2+2x-2y=0，则|x|+|y|的最大值为（ ）
| A． | 2 | B． | 4 | C． | 3$\sqrt{2}$ | D． | 2+$\sqrt{2}$ |
如图，在△ABC中，点P在BC边上，∠PAC=60°，PC=2，AP+AC=4
2．已知函数f（x）=$\frac{1}{3}$x3+a与函数g（x）=$\frac{1}{2}$x2-2x的图象上恰有三对关于y轴对称的点，则实数a的取值范围是（ ）
| A． | （-$\frac{10}{3}$，$\frac{7}{6}$） | B． | （$\frac{7}{6}$，$\frac{10}{3}$） | C． | （-$\frac{7}{6}$，$\frac{10}{3}$） | D． | （-$\frac{10}{3}$，-$\frac{7}{6}$） |
9．
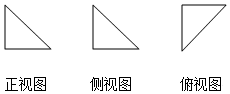已知一个几何体的正视图、侧视图、俯视图都是腰长为1的等腰直角三角形（如图所示），则该几何体的体积是（ ）
已知一个几何体的正视图、侧视图、俯视图都是腰长为1的等腰直角三角形（如图所示），则该几何体的体积是（ ）| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{6}$ |