题目内容
4．极坐标方程ρ2cos 2θ=1表示的曲线是（ ）| A． | 圆 | B． | 双曲线 | C． | 椭圆 | D． | 抛物线 |
分析 极坐标方程ρ2cos 2θ=1转化为ρ2cos2θ-ρ2sin2θ=1，从而化为直角坐标方程得：x2-y2=1．由此能求出结果．
解答 解：∵ρ2cos 2θ=1，
∴ρ2（cos2θ-sin2θ）=1，
∴ρ2cos2θ-ρ2sin2θ=1，
化为直角坐标方程得：x2-y2=1．
∴极坐标方程ρ2cos 2θ=1表示的曲线是双曲线．
故选：B．
点评 本题考查曲线类型的判断，考查极坐标方程与直角坐标方程的互化等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是基础题．
练习册系列答案
相关题目
9．
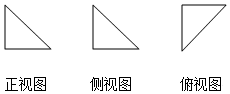已知一个几何体的正视图、侧视图、俯视图都是腰长为1的等腰直角三角形（如图所示），则该几何体的体积是（ ）
已知一个几何体的正视图、侧视图、俯视图都是腰长为1的等腰直角三角形（如图所示），则该几何体的体积是（ ）| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{6}$ |
16．函数f（x）=log2x•log22x取得最小值时x的值为（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\sqrt{2}$ |