题目内容
20.已知f(x)是定义在R上的偶函数,且f(x+4)=f(x-2).若当x∈[-3,0]时,f(x)=6-x,则f(2017)=6.分析 由条件得到函数是周期为6的周期函数,利用函数的周期性和奇偶性进行转化求解即可.
解答 解:由f(x+4)=f(x-2).得f(x+6)=f(x).
即函数是周期为6的周期函数,
则f(2017)=f(336×6+1)=f(1)
∵f(x)是定义在R上的偶函数,且当x∈[-3,0]时,f(x)=6-x,
∴f(1)=f(-1)=6-(-1)=6,
故f(2017)=f(1)=6,
故答案为:6
点评 本题主要考查函数值的计算,根据条件求出函数的周期,利用函数周期性和奇偶性的性质是解决本题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
14.在区间[0,4]内随机选一个实数x,该实数恰好在区间[1,3]内的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
11.某单位有职工480人,其中青年职工210人,中年职工150人,老年职工120人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本,若样本中的青年职工为7人,则样本容量为( )
| A. | 4 | B. | 5 | C. | 7 | D. | 16 |
8.已知实数x,y满足方程x2+y2+2x-2y=0,则|x|+|y|的最大值为( )
| A. | 2 | B. | 4 | C. | 3$\sqrt{2}$ | D. | 2+$\sqrt{2}$ |
9.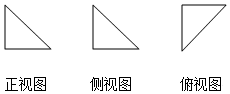 已知一个几何体的正视图、侧视图、俯视图都是腰长为1的等腰直角三角形(如图所示),则该几何体的体积是( )
已知一个几何体的正视图、侧视图、俯视图都是腰长为1的等腰直角三角形(如图所示),则该几何体的体积是( )
 已知一个几何体的正视图、侧视图、俯视图都是腰长为1的等腰直角三角形(如图所示),则该几何体的体积是( )
已知一个几何体的正视图、侧视图、俯视图都是腰长为1的等腰直角三角形(如图所示),则该几何体的体积是( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
 如图,在△ABC中,点P在BC边上,∠PAC=60°,PC=2,AP+AC=4
如图,在△ABC中,点P在BC边上,∠PAC=60°,PC=2,AP+AC=4