题目内容
14.下列命题中,真命题是( )| A. | a-b=0的充要条件是$\frac{a}{b}$=1 | B. | ?x∈R,2x>x | ||
| C. | ?x0∈R,|x0|<0 | D. | 若p∧q为假,则p∨q为假 |
分析 根据题意,判断每一个选项中的命题是否正确.
解答 解:对于A,a-b=0时,$\frac{a}{b}$=1不一定成立,
$\frac{a}{b}$=1时,a-b=0成立,是必要不充分条件,A错误;
对于B,设f(x)=2x-x,x∈R,
∴f′(x)=2xln2-1,
令f′(x)=0,解得x=ln$\frac{1}{ln2}$;
当x<ln$\frac{1}{ln2}$时,f′(x)<0,f(x)单调减;
当x>ln$\frac{1}{ln2}$时,f′(x)>0,f(x)单调增;
∴f(x)的最小值是f(ln$\frac{1}{ln2}$)=$\frac{1}{ln2}$-ln$\frac{1}{ln2}$>0,
∴f(x)=2x-x>0在x∈R上恒成立,
即?x∈R,2x>x恒成立,∴B正确;
对于C,?x∈R,|x|≥0恒成立,∴?x0∈R,|x0|<0错误,即C错误;
对于D,若p∧q为假,则p假、q假或p、q一真一假,∴p∨q为假是错误的.
故选:B.
点评 本题考查了命题真假的判断问题,是综合题.

练习册系列答案
相关题目
2.已知函数f(x)=$\frac{1}{3}$x3+a与函数g(x)=$\frac{1}{2}$x2-2x的图象上恰有三对关于y轴对称的点,则实数a的取值范围是( )
| A. | (-$\frac{10}{3}$,$\frac{7}{6}$) | B. | ($\frac{7}{6}$,$\frac{10}{3}$) | C. | (-$\frac{7}{6}$,$\frac{10}{3}$) | D. | (-$\frac{10}{3}$,-$\frac{7}{6}$) |
9.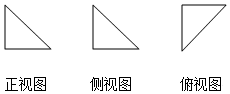 已知一个几何体的正视图、侧视图、俯视图都是腰长为1的等腰直角三角形(如图所示),则该几何体的体积是( )
已知一个几何体的正视图、侧视图、俯视图都是腰长为1的等腰直角三角形(如图所示),则该几何体的体积是( )
 已知一个几何体的正视图、侧视图、俯视图都是腰长为1的等腰直角三角形(如图所示),则该几何体的体积是( )
已知一个几何体的正视图、侧视图、俯视图都是腰长为1的等腰直角三角形(如图所示),则该几何体的体积是( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
 如图,在△ABC中,点P在BC边上,∠PAC=60°,PC=2,AP+AC=4
如图,在△ABC中,点P在BC边上,∠PAC=60°,PC=2,AP+AC=4 正方体ABCD-A1B1C1D1被平面B1D1C截去一部分后得到几何体AB1D1-ABCD.如图所示.
正方体ABCD-A1B1C1D1被平面B1D1C截去一部分后得到几何体AB1D1-ABCD.如图所示.