题目内容
若方程x2-ax+2=0在区间(0,3)内有两个解,则实数a的取值范围是 .
考点:一元二次方程的根的分布与系数的关系
专题:函数的性质及应用
分析:分离参数a=x+
,运用函数图象的交点解决.
| 2 |
| x |
解答:
解:∵方程x2-ax+2=0在区间(0,3)内有两个解,
∴x+
-a=0在区间(0,3)内有两个解,
令f(x)=x+
在区间(0,3)图象如下图:

x+
≥2
,f(3)=3+
=
,
x+
-a=0在区间(0,3)内有两个解,则2
≤a<
,
故答案为:[2
,
)
∴x+
| 2 |
| x |
令f(x)=x+
| 2 |
| x |

x+
| 2 |
| x |
| 2 |
| 2 |
| 3 |
| 11 |
| 3 |
x+
| 2 |
| x |
| 2 |
| 11 |
| 3 |
故答案为:[2
| 2 |
| 11 |
| 3 |
点评:本题综合考察了函数的图象的交点,与方程的根的关系,属于中档题.

练习册系列答案
相关题目
在抛物线y2=8x中,以(1,-1)为中点的弦所在的直线方程为( )
| A、x-4y-3=0 |
| B、x+4y+3=0 |
| C、4x+y-3=0 |
| D、4x+y+3=0 |
已知正项数列{an}的前n项和为Sn,且a1=1,an=
+
(n≥2),则数列{an}的通项公式为an=( )
| Sn |
| Sn+1 |
| A、n-1 | B、n |
| C、2n-1 | D、2n |
已知函数y=2015cos(ωx+φ)(ω>0,0<φ<π),满足f(-x)=-f(x),其图象与直线y=0的某两个交点的横坐标分别为x1,x2,|x1-x2|的最小值为π,则( )
A、ω=2,φ=
| ||
B、ω=2,φ=
| ||
C、ω=1,φ=
| ||
D、ω=1,φ=
|
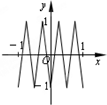
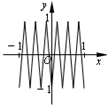
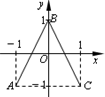 如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=fn(x),n∈N,则函数f4(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=fn(x),n∈N,则函数f4(x)的图象为( )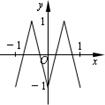
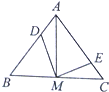 如图,在等腰△ABC中,AB=AC,M为BC中点,点D、E分别在边AB、AC上,且AD=
如图,在等腰△ABC中,AB=AC,M为BC中点,点D、E分别在边AB、AC上,且AD=