Question

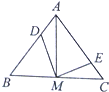如图，在等腰△ABC中，AB=AC，M为BC中点，点D、E分别在边AB、AC上，且AD=

1

2

DB，AE=3EC，若∠DME=90°，则cosA=

 

．

Answer 1

考点：余弦定理的应用

专题：综合题,平面向量及应用

分析：建立如图所示的坐标系，设C（a，0），A（0，b），确定a，b的关系，再利用向量的夹角公式，即可求得结论．

解答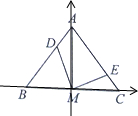： 解：建立如图所示的坐标系，设C（a，0），A（0，b），则D（-

a

3

，

2b

3

），E（

3a

4

，

1

4

b），
∴

MD

=（-

a

3

，

2b

3

），

ME

=（

3a

4

，

1

4

b），
∵∠DME=90°，
∴

MD

•

ME

=0，
∴（-

a

3

，

2b

3

）•（

3a

4

，

1

4

b）=0，
∴-

3a2

12

+

2b2

12

=0
∴a=

6

3

b
∵

AD

=（-

a

3

，-

b

3

），

AE

=（

3a

4

，-

3

4

b），
∴cosA=

- 3a2 12 + 3b2 12

1 3 a2+b2 • 3 4 a2+b2

=

1

5

．
故答案为：

1

5

．

点评：本题考查向量的夹角公式，考查坐标化的运用，考查学生的计算能力，属于中档题．