题目内容

已知数据x1，x2，…，x10的方差为2，且（x1-2）2+（x2-2）2+…+（x10-2）2=110，则数据x1，x2，…，x10的平均数是
 
．
考点：极差、方差与标准差
专题：概率与统计
分析：由已知条件推导出x12+x22+…+x102-10
.
x
2=20，x12+x22+…+x102-40
.
x
+40=110，由此能求出数据x1，x2，…，x10的平均数
.
x
．
解答： 解：∵数据x1，x2，…，x10的方差为2，
∴（x1-
.
x
）2+（x2-
.
x
）2+（x3-
.
x
）2+…+（x10-
.
x
）2=20，
∴x12+x22+…+x102-2
.
x
（x1+x2+…+x10）+10
.
x 
2
=x12+x22+…+x102-10
.
x
2=20，①
∵（x1-2）2+（x2-2）2+…+（x10-2）2=110，
∴x12+x22+…+x102-4（x1+x2+…+x10）+40
=x12+x22+…+x102-40
.
x
+40=110，②
①-②，得40
.
x
-10
.
x
2+50=0，
解得
.
x
=-1或
.
x
=5．
故答案为：-1或5．
点评：本题考查一组数据的平均数的求法，是中档题，解题时要熟练掌握方差的计算公式的灵活运用．
练习册系列答案
相关题目
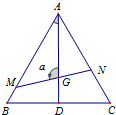如图，△ABC是边长为1的正三角形，M，N分别是边AB，AC上的点，线段MN过△ABC的重心G，设∠MGA=α，α∈[
π
3
，
2π
3
]．
（1）当α=105°时，求MG的长；
（2）分别记△AGM，△AGN的面积为S1，S2，试将S1，S2表示为α的函数；
（3）求y=
1
S12
+
1
S22
的最大值和最小值．
某市2013年4月1日-4月30日对空气污染指数的监测数据如下（主要污染物为可吸入颗粒物）：
61，76，70，56，81，91，92，91，75，81，88，67，101，103，95，91，77，86，81，83，82，82，64，79，86，85，75，71，49，45，
（Ⅰ）完成频率分布表；
（Ⅱ）作出频率分布直方图．
函数f（x）的定义域为D，若存在闭区间[a，b]⊆D，使得函数f（x）满足：（1）f（x）在[a，b]内是单调函数；（2）f（x）在[a，b]上的值域为[ka，kb]，则称区间[a，b]为y=f（x）的“和谐k区间”．
（Ⅰ）若函数f（x）=ex存在“和谐k区间”，求正整数k的最小值；
（Ⅱ）若函数g（x）=
m
2
x2-（m+2）lnx+2x（m≥0）存在“和谐2区间”，求实数m的取值范围．
已知
a
=（
3
sin
x
4
，1），
b
=（cos
x
4
，cos2
x
4
），f（x）=
a
•
b
．
（1）若f（x）=1，求sin（
x
2
+
π
6
）的值；
（2）在△ABC中，若∠B=
π
3
，求函数f（A）的取值范围．
用1，2，3，4，5组成不含重复数字的五位数，数字2不出现在首位和末位，数字1，3，5中有且仅有两个数字相邻，则满足条件的不同五位数的个数是
 
．（注：用数字作答）
过抛物线y2=4x的焦点F作直线交该抛物线于两点A，B，若|AF|=3，则A点的横坐标为
 
．
设各项均不为零的数列{cn}中，所有满足ci•ci+1＜0的正整数i的个数称为这个数列{cn}的变号数．已知数列{an}的前n项和Sn=n2-4n+4，bn=1-
4
an
（n∈N*），则数列{bn}的变号数为
 
．
已知f（2x-1）的定义域为（-1，5]，求函数f（x）的定义域
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网