Question

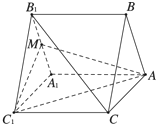如图，三棱柱ABC-A₁B₁C₁的底面是正三角形，AA₁⊥底面ABC，M为A₁B₁的中点．
（Ⅰ）求证：B₁C∥平面AMC₁；
（Ⅱ）若BB₁=5，且沿侧棱BB₁展开三棱柱的侧面，得到的侧面展开图的对角线长为13，求三棱锥B₁-AMC₁的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定

专题：综合题,空间位置关系与距离

分析：（Ⅰ）证明B₁C∥平面AMC₁，只需证明OM∥B₁C；
（Ⅱ）利用转换底面，结合体积公式，即可求三棱锥B₁-AMC₁的体积．

解答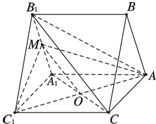： （Ⅰ）证明：如图，连接A₁C，交AC₁于点O，连接OM．…（1分）
∵三棱柱ABC-A₁B₁C₁的侧面是矩形，∴O为A₁C中点，M为A₁B₁的中点，
∴OM∥B₁C．                 …（3分）
又∵OM?平面AMC₁，B₁C?平面AMC₁，
∴B₁C∥平面AMC₁．            …（6分）
（Ⅱ）解∵三棱柱侧面展开图是矩形，且对角线长为13，侧棱BB₁=5，
∴三棱柱底面周长为

132-52

=12，…（7分）
又∵三棱柱的底面是正三角形，
∴A₁C₁=4，B₁M=2，C1M=2

3

，…（9分）
由已知得，S△B1C1M=

1

2

•B1M•C1M=

1

2

×2×2

3

=2

3

，…（10分）
∴VB1-AMC1=VA-B1C1M=

1

3

S△B1C1M•AA1=

1

3

×2

3

×5=

10 3

3

，
即三棱锥B₁-AMC₁的体积为

10 3

3

．             …（12分）

点评：本小题主要考查直线与直线、直线与平面、平面与平面的位置关系、几何体的体积等基础知识；考查空间想象能力、推理论证能力、运算求解能力；考查数形结合思想、化归与转化思想．