题目内容
实数m分别取什么数值时，复数z=（m2+5m+6）+（m2-2m-15）i
（1）是实数；
（2）是虚数；
（3）是纯虚数；
（4）是0．
（1）是实数；
（2）是虚数；
（3）是纯虚数；
（4）是0．
考点：复数的基本概念
专题：数系的扩充和复数
分析：利用复数的基本概念对（1）（2）（3）（4）逐一分析判断即可．
解答：
解：（1）由m2-2m-15=0得：m=5或m=-3时，z为实数…3分
（2）由m2-2m-15≠0，得知：m≠5且m≠-3时，z为虚数…6分
（3）由m2-2m-15≠0，m2+5m+6=0，得知：m=-2时，z为纯虚数…9分
（4）由m2-2m-15=0且m2+5m+6=0，得知：m=-3时，z为0…12分
（2）由m2-2m-15≠0，得知：m≠5且m≠-3时，z为虚数…6分
（3）由m2-2m-15≠0，m2+5m+6=0，得知：m=-2时，z为纯虚数…9分
（4）由m2-2m-15=0且m2+5m+6=0，得知：m=-3时，z为0…12分
点评：本题考查复数的基本概念及其应用，考查方程思想与运算求解能力，属于基础题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
复数z=1+i，则复数z+（
）2012=（ ）
| ||
| z |
| A、1-2i | B、1+2i |
| C、2-i | D、2+i |
已知an=
，则这个数列的前30项中最大项和最小项分别是（ ）
n-
| ||
n-
|
| A、a1，a30 |
| B、a1，a9 |
| C、a10，a30 |
| D、a10，a9 |
已知三棱柱ABC-A1B1C1侧棱与底面垂直，且其六个顶点都在球O的球面上，若AC=3，AB=4，CB=5，球O的半径为6，则OA与平面ABC所成的角的余弦值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
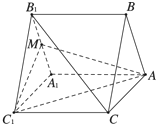如图，三棱柱ABC-A1B1C1的底面是正三角形，AA1⊥底面ABC，M为A1B1的中点．