题目内容
正项数列{an}中,a1=2,a2=8,an2an-2=2an-13(n>3).
(1)设bn=log2
,求证数列{bn}为等比数列,并求通项bn;
(2)设cn=nbn,求数列{cn}的前n项和Tn.
(1)设bn=log2
| an+1 |
| 2an |
(2)设cn=nbn,求数列{cn}的前n项和Tn.
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(1)由已知得
=
,由此能证明数列{bn}是以1为首项,
为公比的等比数列,从而能求出bn=
.
(2)由cn=nbn=
,利用错位相减法能求出数列{cn}的前n项和Tn.
| an2 |
| (2an-1)2 |
| an-1 |
| 2an-2 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
(2)由cn=nbn=
| n |
| 2n-1 |
解答:
解:(1)由已知得
=
,
∴log2
=log2
即2bn-1=bn-2(n>3),
又b1=log2
=1,
∴数列{bn}是以1为首项,
为公比的等比数列.
∴bn=
.…(6分)
(2)∵cn=nbn=
,
∴Tn=
+
+
+
+…+
,
Tn=
+
+
+
+…+
,
两式相减得:
Tn=
+
+
+
+…+
-
=
-
,
∴Tn=4-
.…(12分)
| an2 |
| (2an-1)2 |
| an-1 |
| 2an-2 |
∴log2
| an2 |
| (2an-1)2 |
| an-1 |
| 2an-2 |
又b1=log2
| a2 |
| 2a1 |
∴数列{bn}是以1为首项,
| 1 |
| 2 |
∴bn=
| 1 |
| 2n-1 |
(2)∵cn=nbn=
| n |
| 2n-1 |
∴Tn=
| 1 |
| 20 |
| 2 |
| 21 |
| 3 |
| 22 |
| 4 |
| 23 |
| n |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 21 |
| 2 |
| 22 |
| 3 |
| 23 |
| 4 |
| 24 |
| n |
| 2n |
两式相减得:
| 1 |
| 2 |
| 1 |
| 20 |
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n-1 |
| n |
| 2n |
1-(
| ||
1-
|
| n |
| 2n |
∴Tn=4-
| n+2 |
| 2n-1 |
点评:本题考查等比数列的证明,考查数列的前n项和的求法,考查数列的前n项和的求法,解题时要注意错位相减法的合理运用.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
若ax(1+
)5的展开式中x2项的系数是20,则实数a等于( )
| x |
| A、2 | B、3 | C、4 | D、5 |
已知三棱柱ABC-A1B1C1侧棱与底面垂直,且其六个顶点都在球O的球面上,若AC=3,AB=4,CB=5,球O的半径为6,则OA与平面ABC所成的角的余弦值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:

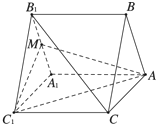 如图,三棱柱ABC-A1B1C1的底面是正三角形,AA1⊥底面ABC,M为A1B1的中点.
如图,三棱柱ABC-A1B1C1的底面是正三角形,AA1⊥底面ABC,M为A1B1的中点.