题目内容
已知tanα=-
,求:sinα,cosα.
| 3 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:由tanα的值小于0,得到α为第二或第四象限角,利用同角三角函数间的基本基本关系求出sinα与cosα的值即可.
解答:
解:∵tanα=
=-
,
∴sinα=-
cosα,
∵sin2α+cos2α=1,∴3cos2α+cos2α=1,
∴cos2α=
,
又tanα=-
<0,
∴α只可能为第二象限角或第四象限角,
当α为第二象限角时,cosα=-
,sinα=
;
当α为第四象限角时,cosα=
,sinα=-
.
| sinα |
| cosα |
| 3 |
∴sinα=-
| 3 |
∵sin2α+cos2α=1,∴3cos2α+cos2α=1,
∴cos2α=
| 1 |
| 4 |
又tanα=-
| 3 |
∴α只可能为第二象限角或第四象限角,
当α为第二象限角时,cosα=-
| 1 |
| 2 |
| ||
| 2 |
当α为第四象限角时,cosα=
| 1 |
| 2 |
| ||
| 2 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
已知an=
,则这个数列的前30项中最大项和最小项分别是( )
n-
| ||
n-
|
| A、a1,a30 |
| B、a1,a9 |
| C、a10,a30 |
| D、a10,a9 |
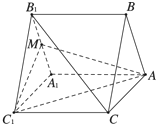 如图,三棱柱ABC-A1B1C1的底面是正三角形,AA1⊥底面ABC,M为A1B1的中点.
如图,三棱柱ABC-A1B1C1的底面是正三角形,AA1⊥底面ABC,M为A1B1的中点.