题目内容
已知a∈R,函数f(x)=x2+ax-lnx,g(x)=ex.(其中e是自然对数的底数)
(1)当a=-1时,求函数y=f(x)的极值;
(2)令F(x)=
,若函数F(x)在区间(0,1]上是单调函数,求a的取值范围.
(1)当a=-1时,求函数y=f(x)的极值;
(2)令F(x)=
| f(x) |
| g(x) |
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)求出函数f(x)的导数,利用导数的正负性判断单调性,从而求函数的极值;
(2)求出F(x)的导数,化简构造函数h(x),求出h(x)的导数,讨论函数h′(x)正负性,判断h(x)的单调性,根据h(x)的正负性,判断F(x)的单调性,从而求出参数a的取值范围.
(2)求出F(x)的导数,化简构造函数h(x),求出h(x)的导数,讨论函数h′(x)正负性,判断h(x)的单调性,根据h(x)的正负性,判断F(x)的单调性,从而求出参数a的取值范围.
解答:
解:(1)当a=-1时,f(x)=x2-x-lnx,定义域为(0,+∞),
∴f′(x)=2x-1-
=
=
,
∴当0<x<1,时f′(x)<0,当x>1时,f′(x)>0,
∴f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
∴在x=1时,f(x)有极小值,且极小值f(x)=f(1)=0;
(2)F(x)=
=
,定义域为(0,+∞),
F′(x)=
,
令h(x)=-x2+(2-a)x+a-
+lnx,则h′(x)=-2x+
+
+2-a,
h″(x)=-2-
-
<0,故h′(x)在区间(0,1]上单调递减,
从而对(0,1],h′(x)≥h′(1)=2-a
①当2-a≥0,即a≤2时,h′(x)≥0,∴y=h(x)在区间(0,1]上单调递增,
∴h(x)≤h(1)=0,即F′(x)≤0,
∴y=F(x)在区间(0,1]上是减函数,a≤2满足题意;
②当2-a<0,即a>2时,由h′(1)<0,h′(
)=-
+a2+2>0,0<
<1,
且y=h′(x)在区间(0,1]的图象是一条连续不断的曲线,
∴y=h′(x)在区间(0,1]有唯一零点,设为x0,
∴h(x)在区间(0,x0)上单调递增,在(x0,1]上单调递减,
∴h(x0)>h(1)=0,而h(e-a)=-e-2a+(2-a)e-a+a-ea+lne-a<0,
且y=h(x)在区间(0,1]的图象是一条连续不断的曲线,
y=h(x)在区间(0,1)有唯一零点,设为x′,
即y=F′(x)在区间(0,1)有唯一零点,设为x′,
又F(x)在区间(0,x′)上单调递减,在(x′,1)上单调递增,
矛盾,a>2不合题意;
综上所得:a的取值范围为(-∞,2].
∴f′(x)=2x-1-
| 1 |
| x |
| 2x2-x-1 |
| x |
| (x-1)(2x+1) |
| x |
∴当0<x<1,时f′(x)<0,当x>1时,f′(x)>0,
∴f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
∴在x=1时,f(x)有极小值,且极小值f(x)=f(1)=0;
(2)F(x)=
| f(x) |
| g(x) |
| x2+ax-lnx |
| ex |
F′(x)=
-x2+(2-a)x+a-
| ||
| ex |
令h(x)=-x2+(2-a)x+a-
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
h″(x)=-2-
| 1 |
| x3 |
| 1 |
| x2 |
从而对(0,1],h′(x)≥h′(1)=2-a
①当2-a≥0,即a≤2时,h′(x)≥0,∴y=h(x)在区间(0,1]上单调递增,
∴h(x)≤h(1)=0,即F′(x)≤0,
∴y=F(x)在区间(0,1]上是减函数,a≤2满足题意;
②当2-a<0,即a>2时,由h′(1)<0,h′(
| 1 |
| a |
| 2 |
| a |
| 1 |
| a |
且y=h′(x)在区间(0,1]的图象是一条连续不断的曲线,
∴y=h′(x)在区间(0,1]有唯一零点,设为x0,
∴h(x)在区间(0,x0)上单调递增,在(x0,1]上单调递减,
∴h(x0)>h(1)=0,而h(e-a)=-e-2a+(2-a)e-a+a-ea+lne-a<0,
且y=h(x)在区间(0,1]的图象是一条连续不断的曲线,
y=h(x)在区间(0,1)有唯一零点,设为x′,
即y=F′(x)在区间(0,1)有唯一零点,设为x′,
又F(x)在区间(0,x′)上单调递减,在(x′,1)上单调递增,
矛盾,a>2不合题意;
综上所得:a的取值范围为(-∞,2].
点评:本题考查的是利用导数求函数的极值,同时考查了利用导数解决参数问题,利运用了二次求导,是一道导数的综合性问题.属于难题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
已知三棱柱ABC-A1B1C1侧棱与底面垂直,且其六个顶点都在球O的球面上,若AC=3,AB=4,CB=5,球O的半径为6,则OA与平面ABC所成的角的余弦值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
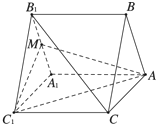 如图,三棱柱ABC-A1B1C1的底面是正三角形,AA1⊥底面ABC,M为A1B1的中点.
如图,三棱柱ABC-A1B1C1的底面是正三角形,AA1⊥底面ABC,M为A1B1的中点.