题目内容
点F1，F2是两定点，动点P满足|PF1|-|PF2|=a（a为常数），则动点P的轨迹是（ ）
| A、射线 | B、双曲线 |
| C、不存在 | D、可能是双曲线的一支 |
考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据双曲线的定义可得结论．
解答：
解：点F1，F2是两定点，动点P满足|PF1|-|PF2|=a（a为常数），若a＜|F1F2|，则动点P的轨迹是双曲线的一支．
故选：D．
故选：D．
点评：本题主要考查了双曲线的定义，轨迹方程问题．考查了学生对基础知识的综合运用．
练习册系列答案
相关题目
复数z=1+i，则复数z+（
）2012=（ ）
| ||
| z |
| A、1-2i | B、1+2i |
| C、2-i | D、2+i |
若ax（1+
）5的展开式中x2项的系数是20，则实数a等于（ ）
| x |
| A、2 | B、3 | C、4 | D、5 |
各项均为正数的数列{an}，{bn}满足：an+2=2an+1+an，bn+2=bn+1+2bn（n∈N*），那么（ ）
| A、?n∈N*，an＞bn⇒an+1＞bn+1 |
| B、?m∈N*，?n＞m，an=bn |
| C、?m∈N*，?n＞m，an＞bn |
| D、?m∈N*，?n＞m，an＜bn |
在△ABC中，若对任意的λ∈R，都有|
+λ
|≥|
|，则△ABC（ ）
| AB |
| AC |
| BC |
| A、一定为锐角三角形 |
| B、一定为钝角三角形 |
| C、一定为直角三角形 |
| D、可以为任意三角形 |
已知an=
，则这个数列的前30项中最大项和最小项分别是（ ）
n-
| ||
n-
|
| A、a1，a30 |
| B、a1，a9 |
| C、a10，a30 |
| D、a10，a9 |
已知三棱柱ABC-A1B1C1侧棱与底面垂直，且其六个顶点都在球O的球面上，若AC=3，AB=4，CB=5，球O的半径为6，则OA与平面ABC所成的角的余弦值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
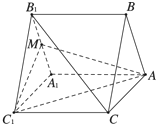如图，三棱柱ABC-A1B1C1的底面是正三角形，AA1⊥底面ABC，M为A1B1的中点．