题目内容
已知平行四边形的3个顶点为A（a，b），B（-b，a），C（0，0），则它的第4个顶点D的坐标是（ ）
| A、（2a，b） |
| B、（a+b，b-a） |
| C、（a-b，a+b） |
| D、（a-b，b-a） |
考点：平行向量与共线向量
专题：平面向量及应用
分析：利用平行四边形的性质、向量相等、向量的坐标运算即可得出．
解答：
解：由平行四边形可得
=
，
∴
=
-
=（0，0）-[（-b，a）-（a，b）]=（a+b，b-a）．
故选：B．
| DC |
| AB |
∴
| OD |
| OC |
| AB |
故选：B．
点评：本题考查了平行四边形的性质、向量相等、向量的坐标运算，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
利用不等式求最值，下列运用错误的是（ ）
A、若x＜-1，则2x-1+
| ||||
B、
| ||||
C、y=2x+
| ||||
D、已知ab＞0，
|
已知曲线C的参数方程为
（t为参数），则点M1（0，1），M2（5，4）与曲线C的位置关系是（ ）
|
| A、M1在曲线C上，但M2不在 |
| B、M1不在曲线C上，但M2在 |
| C、M1，M2都在曲线C上 |
| D、M1，M2都不在曲线C上 |
设cos（
-α）=
，则sin2α=（ ）
| π |
| 4 |
| 1 |
| 3 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
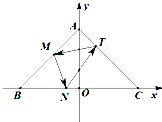如图，点A，B，C的坐标分别为（0，2），（-2，0），（2，0），点M是边AB上异于A，B的一点，光线从点M出发，经BC，CA反射后又回到起点M．若光线NT交y轴于点（0，| 2 |
| 3 |
A、（-
| ||||
B、（-
| ||||
| C、（-1，1） | ||||
D、（-
|
已知离散型随机变量X的分布列如表，则常数q=（ ）
| X | 0 | 1 | 2 |
| P | 0.5 | 1-2q | q2 |
A、1+
| ||||
B、1-
| ||||
C、1±
| ||||
D、
|
已知f（x）=
，则f′（
）等于（ ）
| sinx |
| sinx+cosx |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|